Pattern Self-Assembly
When designing a self-assembling system, the desired goal is often the creation of an assembly with a target shape. However, it may instead be an assembly that serves as surface onto which a desired pattern of cargo molecules are attached. In the domain of the aTAM, this problem is typically represented as the problem of weakly self-assembling a pattern of colored tiles, which can be thought of as forming structures on which colored patterns are “painted.” Here we discuss results related to the complexity, in terms of the unique tile types required, of assembling various patterns. The following results are generally concerned with the optimal complexity of construction of \(n \times n\) patterns. However, the problem of designing optimal tile sets to self-assemble patterned squares, the PATS problem, has also been widely studied.
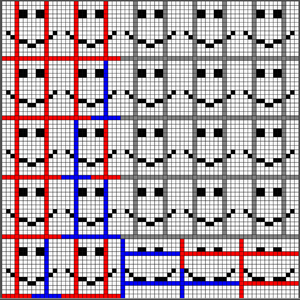
We first discuss constructions for three different ``simple patterns. A single-pixel pattern is a pattern where a single tile is set to black. A multi-pixel pattern is a pattern with a set of locations set to black such that the locations are \((\log n)\) distance away from each other. A striped pattern is a pattern where black stripes repeat themselves every \(i\) times horizontally and \(j\) times vertically. All three types of pattern can be built using \(O(\log n)\) tile types making relatively straightforward use of binary counters.
This paper also shows that for almost all positive integers \(n\), the tile complexity of weakly self-assembling 2-colored patterns on a \(n x n\) squares in the aTAM is \(\Theta(\frac{n^2}{\log n})\). This is done by proving this is lower bound for almost all patterns and by providing a construction for building any \(n x n\) square.
2-colored patterns on an \(n x n\) square may be exhibited in the attached software "tiled_images", with usage instructions described in the README.
This paper also shows that almost any pattern \(p_n\) may be generated such that \(O (\frac{\log n} {\log \log n})\) tile types are required. And there exist patterns, both finite and infinite, that can be weakly self-assembled using asymptotically fewer tile types using barely-3DaTAM systems than by regular, 2D aTam Systems.
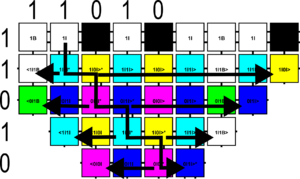
A pattern consists of a bit-sequence of length \(m\) such that the north row, and west column of an \(mxm\) square are made up of that tile representing that bit sequence of length \(m\), with colors associated being either \(\{White, Green, Black\}\) or \(\{Red, Green, Black\}\). Each bound propagates a signal which interacts with the bound on its perpendicular, creating an intersection between the two bits \(\{00, 01, 10, 11\}\). Each intersection is assigned its own color within the interior along \(\{Aqua, Blue, Yellow, Fuchsia\}\).
Patterns may be generated in the 2D plane using \(O( \frac{\log n} {\log \log n})\) tile types, and it has been proven that this is the most efficient way to generate almost all patterns. This is done through the exhibition of pattern \(p_n\) such that every 2D aTAM system, \(\mathcal{T}_{\le n}\), with fewer than \(n\) tile types fails to weakly self-assemble \(p_n\). For each \(\mathcal{T}_{\le n}\), \(p_n\) is defined in such a way that its color differs in at least one location in each “cell” of a repeating grid of cells.
Patterns generated within 2D aTAM systems, and barely-3DaTAM systems may be exhibited in the attached software “2_layer_patterns”, with usage instructions detailed in the README.
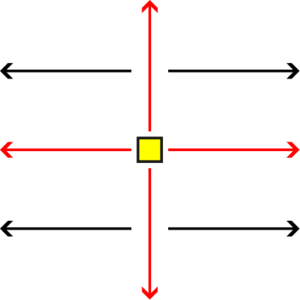
These patterns may be extended to infinitely cover the 2D plane in a cross-like shape through the use of grid-reconstruction utilizing \(O(1)\) unique tile type, with subsequent patterns copying themselves along the cross-like shape, as is described in the below figure Any bit-sequence of length \(n\) may be constructed to tile both finitely, or infinitely through the use of the attached piece of software “infinite_tiling_patterns”, with usage instructions detailed in the README.
A set of Python and Java programs that generate aTAM systems related to these constructions, as well as example systems, can be downloaded here:
SelfAssembledPatterns code (Note that the latest version can be found at the bottom of the list.)