Difference between revisions of "Pattern Self-Assembly"
| Line 17: | Line 17: | ||
|- | |- | ||
| [[File:SinglePixel.png|thumb|center|A single black tile]] | | [[File:SinglePixel.png|thumb|center|A single black tile]] | ||
| − | | [[File:MultiPixel.png|thumb|center|Multiple black tiles | + | | [[File:MultiPixel.png|thumb|center|Multiple black tiles]] |
| − | | [[File:StripesPattern.png|thumb|center|Repeating black tiles | + | | [[File:StripesPattern.png|thumb|center|Repeating black tiles]] |
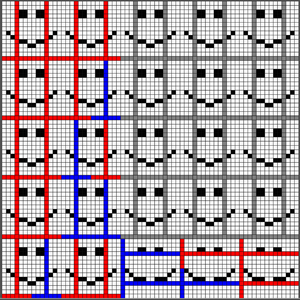
| − | | [[File:GridRepeat.png|thumb|center| | + | | [[File:GridRepeat.png|thumb|center|A repeated pattern in a grid. The spines are colored to show the counter values embedded in them. Red mean 1 and blue mean 0]] |
|} | |} | ||
| Line 30: | Line 30: | ||
| [[File:SkeletonFilled1.png|thumb|center|The square once the ribs of the skeleton have filled in (blue growing left, yellow growing right)]] | | [[File:SkeletonFilled1.png|thumb|center|The square once the ribs of the skeleton have filled in (blue growing left, yellow growing right)]] | ||
|} | |} | ||
| + | |||
| + | This paper also shows that almost any $nxn$ pattern $p_n$ may be generated such that $O \frac{\log n} {\log \log n}$ tile types are required. And there exist patterns, both finite and infinite, that can be weakly self-assembled using asymptotically fewer tile types using barely-3DaTAM systems than by regular, 2D aTam Systems. | ||
| + | |||
| + | A pattern consists of a string of 0’s and 1’s $n$ such that the north row, and west column of an $nxn$ square are made up of that pattern $n$, with colors associated being either $\{White, Green, Black\}$ or $\{Red, Green, Black\}$. Each bound propagates a signal which interacts with the bound on its perpendicular, creating an intersection between the two bits $\{00, 01, 10, 11\}$. Each intersection is assigned its own color within the interior along $\{Aqua, Blue, Yellow, Fuchsia\}$. | ||
| + | |||
| + | Patterns may be generated in the 2D plane using $O( \frac{\log n} {\log \log n})$ tile types, and it has been proven that this is the most efficient way to generate almost all patterns. This is done through the exhibition of pattern $p_n$ such that every 2D aTAM system, $\mathcal{T}_{\le n}$, with fewer than $n$ tile types fails to weakly self-assemble $p_n$. For each $\mathcal{T}_{\le n}$, $p_n$ is defined in such a way that its color differs in at least one location in each “cell” of a repeating grid of cells. | ||
Revision as of 15:49, 3 March 2024
Abstract
In the abstract Tile Assembly Model, self-assembling systems consisting of tiles of different colors can form structures on which colored patterns are “painted.” We explore the complexity, in terms of the unique tile types required, of assembling various patterns, proving several upper and lower bounds.
Overview
This paper concerns itself with the optimal complexity of construction of nxn patterns.
We first show constructions for three different simple patterns. A single-pixel pattern is a pattern where a single tile is set to black. A multi-pixel pattern is a pattern with a set of locations set to black such that the locations are \((\log n)\) distance away from each other. A striped pattern is a pattern where black stripes repeat themselves every \(i\) times horizontally and \(j\) times vertically. This paper provides constructions for each of these that use \(O(\log n)\) tile types.
This paper also shows that for almost all positive integers n, the tile complexity of weakly self-assembling 2-colored patterns on a n × n squares in the aTAM is \(\Theta(\frac{n^2}{\log n})\). This is done by proving this is lower bound for almost all patterns and by providing a construction for building any n x n square.
This paper also shows that almost any \(nxn\) pattern \(p_n\) may be generated such that \(O \frac{\log n} {\log \log n}\) tile types are required. And there exist patterns, both finite and infinite, that can be weakly self-assembled using asymptotically fewer tile types using barely-3DaTAM systems than by regular, 2D aTam Systems.
A pattern consists of a string of 0’s and 1’s \(n\) such that the north row, and west column of an \(nxn\) square are made up of that pattern \(n\), with colors associated being either \(\{White, Green, Black\}\) or \(\{Red, Green, Black\}\). Each bound propagates a signal which interacts with the bound on its perpendicular, creating an intersection between the two bits \(\{00, 01, 10, 11\}\). Each intersection is assigned its own color within the interior along \(\{Aqua, Blue, Yellow, Fuchsia\}\).
Patterns may be generated in the 2D plane using \(O( \frac{\log n} {\log \log n})\) tile types, and it has been proven that this is the most efficient way to generate almost all patterns. This is done through the exhibition of pattern \(p_n\) such that every 2D aTAM system, \(\mathcal{T}_{\le n}\), with fewer than \(n\) tile types fails to weakly self-assemble \(p_n\). For each \(\mathcal{T}_{\le n}\), \(p_n\) is defined in such a way that its color differs in at least one location in each “cell” of a repeating grid of cells.
A set of Python and Java programs that generate aTAM systems related to these constructions, as well as example systems, can be downloaded here:
SelfAssembledPatterns code (Note that the latest version can be found at the bottom of the list.)