Tile Automata
Contents
Abstract
Self-assembly is the process by which a system of particles randomly agitate and combine, through local interactions, to form larger complex structures. In this work, we fuse a particular well-studied generalization of tile assembly (the 2-Handed or Hierarchical Tile Assembly Model) with concepts from cellular automata such as states and state transitions characterized by neighboring states. This allows for a simplification of the concepts from active self-assembly, and gives us machinery to relate the disparate existing models. We show that this model, coined Tile Automata, is invariant with respect to freezing and non-freezing transition rules via a simulation theorem showing that any non-freezing tile automata system can be simulated by a freezing one. Freezing tile automata systems restrict state transitions such that each tile may visit a state only once, i.e., a tile may undergo only a finite number of transitions. We conjecture that this result can be used to show that the Signal-passing Tile Assembly Model is also invariant to this constraint via a series of simulation results between that model and the Tile Automata model. Further, we conjecture that this model can be used to consolidate the several oft-studied models of self-assembly wherein assemblies may break apart, such as the Signal-passing Tile Assembly Model, the negative-glue 2-Handed Tile Assembly Model, and the Size-Dependent Tile Assembly Model. Lastly, the Tile Automata model may prove useful in combining results in cellular automata with self-assembly.
Model Overview
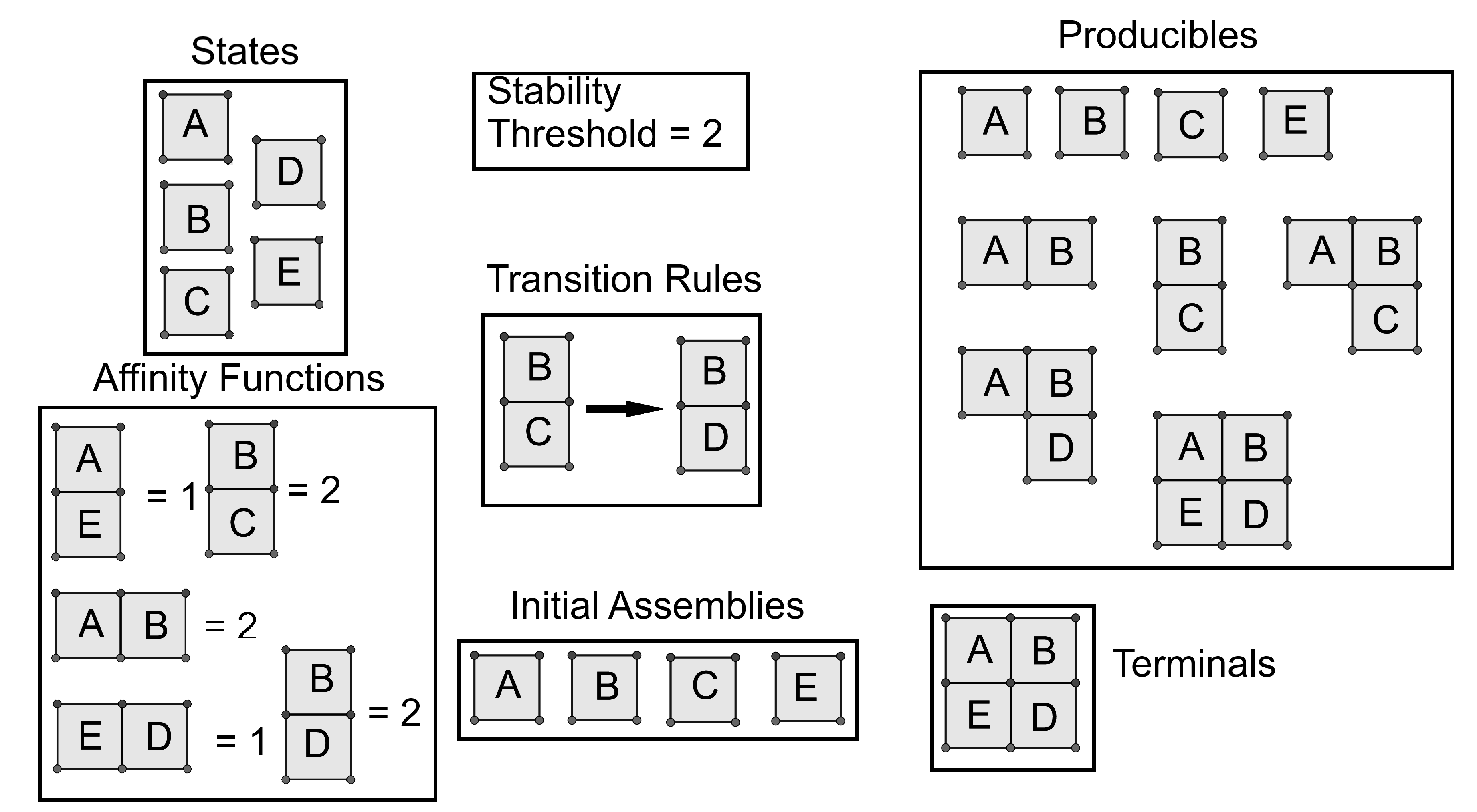
Tiles and States - Consider an alphabet of state types, called Σ. A tile t is an axis-aligned unit square centered at a point L(t)∈Z2 . Further, tiles are assigned a state type from Σ, where S(t) denotes the state type for a given tile t. We say two tiles t1 and t2 are of the same tile type if S(t1)=S(t2).
Affinity Function - An affinity function takes as input an element in Σ2×D, where D={⊥,⊢}, and outputs an element in N. This output is referred to as the affinity strength between two states, given direction d∈D. Directions ⊥ and ⊢ indicate above-below and side-by-side orientations of states, respectively.
Transition Rules - Transition rules allow states to change based on their neighbors. Formally, a transition rule is a 5-tuple (S1a,S2a,S1b,S2b,d) with each S1a,S2a,S1b,S2b∈Σ and d∈D={⊥,⊢}. Essentially, a transition rule says that if states S1a and S2a are adjacent to each other, with a given orientation d, they can transition to states S1b and S2b respectively.
Assemblies - A positioned shape is any subset of Z2. A positioned assembly is a set of tiles at unique coordinates in Z2, and the positioned shape of a positioned assembly A is the set of coordinates of those tiles, denoted as SHAPEA. For a positioned assembly A, let A(x,y) denote the state type of the tile with location (x,y)∈Z2 in A.
Breakable Assemblies - An assembly is τ-breakable if it can be split into two assemblies along a cut whose total affinity strength sums to less than τ. Formally, an assembly C is breakable into assemblies A and B if the bond graph GC for some positioned assembly C∈C has a cut (A,B) for positioned assemblies A∈A and B∈B of affinity strength less than τ. We call assemblies A and B pieces of the breakable assembly C.
Combinable Assemblies - Two assemblies are τ-combinable provided they may attach along a border whose strength sums to at least τ. Formally, two assemblies A and B are τ-combinable into an assembly C provided GC for any C∈C has a cut (A,B) of strength at least τ for some positioned assemblies A∈A and B∈B. We call C a combination of A and B.
Transitionable Assemblies - Consider some set of transition rules Δ. An assembly A is transitionable, with respect to Δ, into assembly B if and only if there exist A∈A and B∈B such that for some pair of adjacent tiles ti,tj∈A:
- ∃ a pair of adjacent tiles th,tk∈B with L(ti)=L(th) and L(tj)=L(tk)
- ∃ a transition rule δ∈Δ s.t. δ=(S(ti),S(tj),S(th),S(tk),⊥)
or
δ=(S(ti),S(tj),S(th),S(tk),⊢)
A−{ti,tj}=B−{th,tk}
A tile automata system is a 5-tuple (Σ,Π,Λ,Δ,τ) where Σ is an alphabet of state types, Π is an affinity function, Λ is a set of initial assemblies with each tile assigned a state from Σ, Δ is a set of transition rules for states in Σ, and τ∈N is the stability threshold. When the affinity function and state types are implied, let (Λ,Δ,τ) denote a tile automata system.
Results
It was proven in [1], which also introduced the model, that a variant of Tile Automata systems where tiles may only visit any given state once is capable of simulating TA systems with reusable states. This introduced the concept of "freezing" TA, which is bounded to a finite number of state changes and showed how freezing TA can simulate non freezing TA, scaled in space, time, and a polynomial scaling in state complexity. Another result shows how to use a 100 tile macrotile replacement schema to simulate arbitrary Amoebot systems. TODO: ADD CITATION AFTER PUBLICATION IN DNA 25
References
- ↑
Chalk, Cameron, Luchsinger, Austin, Martinez, Eric, Schweller, Robert, Winslow, Andrew, Wylie, Tim - Freezing Simulates Non-freezing Tile Automata
- International Conference on DNA Computing and Molecular Programming pp. 155--172,2018
- BibtexAuthor : Chalk, Cameron, Luchsinger, Austin, Martinez, Eric, Schweller, Robert, Winslow, Andrew, Wylie, Tim
Title : Freezing Simulates Non-freezing Tile Automata
In : International Conference on DNA Computing and Molecular Programming -
Address :
Date : 2018