Amoebots

The amoebot model is an abstract computational model of programmable matter intended to enable rigorous algorithmic analysis of collective systems at the nano-scale. In the amoebot model, programmable matter consists of individual, homogeneous computational elements called particles. Any structure that a particle system can form is represented as a subgraph of an infinite, undirected graph \(G= (V, E)\) where \(V\) represents all positions a particle can occupy relative to its structure and \(E\) represents all atomic movements a particle can make. Each node in \(V\) can be occupied by at most one particle at a time. In the geometric amoebot model, we further assume that \(G=G∆\), where \(G∆\) is the triangular lattice. Fixing the position of some particle,\(G∆\) represents the discretization of space relative to this particle and the possible atomic movements between these discrete positions. This discretization can be conceptualized as a tiling of two-dimensional space; \(G∆\) corresponds to the hexagonal tiling.

Model Overview

Each particle occupies either a single node in \(V\)(i.e., it is contracted) or a pair of adjacent nodes in \(V\) (i.e., it is expanded), as in Fig. 3b. Two particles occupying adjacent nodes of \(G∆\) are called neighbors. Each particle keeps a collection of ports one for each edge incident to the node(s) it occupies — that have unique labels from its own perspective. Contracted particles have six ports while expanded particles have ten (see Fig. 3c). The particles are assumed to have a common sense of clockwise direction (a.k.a. chirality), but do not share a coordinate system or global compass. Thus, particles can label their ports in clockwise order starting from a local direction 0,but may have different orientations in O = {0, 1,..., 5} encoding their offsets for local direction 0 from global direction 0 (to the right).

(a) A section of the triangular lattice \(G∆\) (black) and its dual, the hexagonal tiling (gray). (b) Expanded and contracted particles (black dots) on \(G∆\) (gray lattice). Particles with a black line between their nodes are expanded. (c) Two particles with different orientations. The expanded particle’s tail port would be 6 if its head were the upper node; the contracted particle’s tail port is ε.

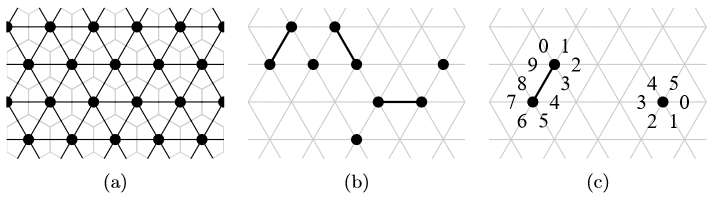
Particles move via a series of expansions and contractions: a contracted particle can expand into an unoccupied adjacent node to become expanded, and may then contract to occupy a single node once again. An expanded particle’s head is the node it last expanded into and the other node it occupies is its tail; a contracted particle’s head and tail are the same. If an expanded particle contracts into its head node, it has moved. Otherwise, contracting back into its tail node can be thought of as the particle exploring a potential location to which it could expand but deciding not to over the course of two activations. Neighboring particles can coordinate their movements in a handover, which can occur one of two ways. A contracted particle p can “push” an expanded neighbor q by expanding into one of the nodes occupied by q, forcing q to contract. Alternatively, an expanded particle q can “pull” a contracted neighbor p by contracting, forcing p to expand into the node it is vacating. During its movements, each particle maintains a tail port in T = {0, 1, ... ,9} ∪{ε} denoting the port furthest from its head if it is expanded or ε if it is contracted. This information serves as the particle’s memory about whether or not it is expanded, and, if so, what direction its tail is relative to its head.

Results

Work on the Amoebot model has produced a number of interesting results pertaining to distributed, locally constrained algorithms and swarm dynamics. Algorithms have been presented for object coating , bridging gaps , and more.

An image showing the natural motivation for studying bridging algorithms, and an image of amoebot particles successfully emulating such behavior using only local information.