Difference between revisions of "Shape Replication"

From self-assembly wiki
Jump to navigation Jump to search
Line 10: Line 10:
  
 
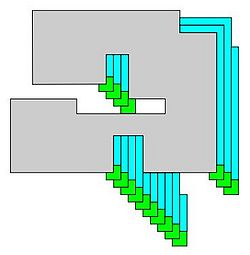
In a paper by Hendricks, Patitz, and Rogers<ref name="SPT"/>, it is shown that replication can be achieved in the signal-passing tile assembly model. This method of replication starts by creating a frame around the input shape, which, after the frame tiles have verified that the shape is completely covered, breaks off of the input assembly and exposes new glues for the replicated assembly to start growth from.
 
In a paper by Hendricks, Patitz, and Rogers<ref name="SPT"/>, it is shown that replication can be achieved in the signal-passing tile assembly model. This method of replication starts by creating a frame around the input shape, which, after the frame tiles have verified that the shape is completely covered, breaks off of the input assembly and exposes new glues for the replicated assembly to start growth from.
 +
 +
{{multiple image
 +
| align = center
 +
| width = 250
 +
| footer = How shape replication in the signal passing tile assembly system works.
 +
| image1 = stam_replication_phase_one.jpg
 +
| alt1 = Phase One
 +
| caption1 = Replication starts by attaching tiles to any southeast, convex verticies.
 +
| image2 = stam_replication_phase_two.jpg
 +
| alt2 = Phase Two
 +
| caption2 = The tiles keep growing around the shape until they make a rectangle.
 +
}}
  
 
==References==
 
==References==

Revision as of 10:36, 14 July 2016

Overview

Replication is the concept of having a tile assembly system that can take input shapes and create new instances of that shape using a constant sized tile set.

Replication Using RNAse

In a paper by Abel, Benbernou, Damian, Demaine, Demaine, Flatland, Kominers, and Schweller[1], it is shown that replication can be achieved using an RNase augmentation of the staged tile assembly model. The shapes that their methods are limited to are arbitrary genus 0 shapes with minimum features of at least 5. Their first result showed that shapes can be replicated precisely n times using O(log n) stages and a constant number of tile types. This result works by... Their second result showed that shapes can be replicated indefinitely using a constant number of stages and a constant number of tile types. This result works by...

Replication Using Signal Passing Tiles

In a paper by Hendricks, Patitz, and Rogers[2], it is shown that replication can be achieved in the signal-passing tile assembly model. This method of replication starts by creating a frame around the input shape, which, after the frame tiles have verified that the shape is completely covered, breaks off of the input assembly and exposes new glues for the replicated assembly to start growth from.

Phase One
Replication starts by attaching tiles to any southeast, convex verticies.
Phase Two
The tiles keep growing around the shape until they make a rectangle.
How shape replication in the signal passing tile assembly system works.

References

  1. ↑ Zachary Abel, Nadia Benbernou, Mirela Damian, Erik D. Demaine, Martin L. Demaine, Robin Flatland, Scott D. Kominers,, Robert Schweller - Shape Replication through Self-Assembly and RNase Enzymes
    ACM-SIAM Symposium on Discrete Algorithms ,2010
    Bibtex
    Author : Zachary Abel, Nadia Benbernou, Mirela Damian, Erik D. Demaine, Martin L. Demaine, Robin Flatland, Scott D. Kominers,, Robert Schweller
    Title : Shape Replication through Self-Assembly and RNase Enzymes
    In : ACM-SIAM Symposium on Discrete Algorithms -
    Address :
    Date : 2010
  2. ↑ Jacob Hendricks, Matthew J. Patitz,, Trent A. Rogers - Replication of arbitrary hole-free shapes via self-assembly with signal-passing tiles
    aiXiv (1503.01244),2015
    Bibtex
    Author : Jacob Hendricks, Matthew J. Patitz,, Trent A. Rogers
    Title : Replication of arbitrary hole-free shapes via self-assembly with signal-passing tiles
    In : aiXiv -
    Address :
    Date : 2015
Retrieved from "http://self-assembly.net/wiki/index.php?title=Shape_Replication&oldid=1358"