Shape Replication

Overview

Replication is the concept of having a tile assembly system that can take input shapes and create new instances of that shape using a fixed tile set.

Replication Using RNAse

In a paper by Abel, Benbernou, Damian, Demaine, Demaine, Flatland, Kominers, and Schweller, it is shown that replication can be achieved using an RNase augmentation of the staged tile assembly model. The shapes that their methods are limited to are arbitrary genus 0 shapes with minimum features of at least 5, meaning the length between any two, non-adjacent edges must be at least 5 units. Their first result showed that shapes can be replicated precisely n times using O(log n) stages and a constant number of tile types. This result works by first creating an RNA frame around the input shape and then creating a second DNA frame around the RNA frame. RNase is then added to the solution to dissolve the RNA frame and leave the input shape and the DNA frame behind. The process is repeated in reverse, allowing RNA to bind to the DNA frame and more DNA tiles to attach inside the RNA frame, after which RNase is put into the solution again to break off the replica shape. Tiles can then, optionally, be added to the DNA frame to disallow it from interacting with any additional tiles, rendering it unable to spawn more replicas of the original shape, thereby helping to control the replication to the desired amount.

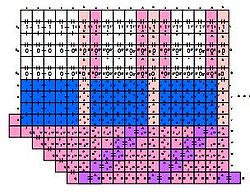
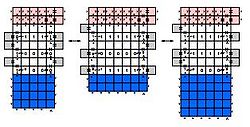
Their second result showed that shapes can be replicated indefinitely using a constant number of stages and a constant number of tile types. This result works by first, engulfing the shape in a rectangle and filling in the spaces between the shape and the outside rectangle. This original model is then broken up into sections. Each section then builds an indefinite number of copies of itself, which come together using special "teeth" tiles on their edges to make an indefinite number of instances of the original mold. Each mold then fills in with an instance of the original shape, which is then broken off by adding RNase, leaving an indefinite number of instances of the original shape.

The process starts by creating the original mold around the input shape.

The original mold breaks apart and an indefinite number of replicas of each section are built

The sections come together using special edges and create an indefinite number of molds

The steps involved in the indefinite replication result.

Replication Using Signal Passing Tiles

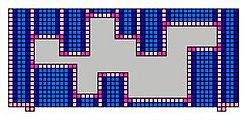
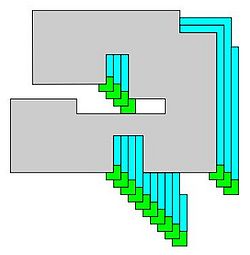
In a paper by Hendricks, Patitz, and Rogers, it is shown that replication can be achieved in the signal-passing tile assembly model. This method of replication starts by creating a frame around the input shape. This starts when small supertiles are placed at each southeast convex corner of the shape. Tile then grow counter-clockwise around the shape, stopping at concavities. New paths of tiles keep growing until eventually, one path is able to grow a complete rectangle around the shape and crash back into the original supertile that spawned the path's growth. This process is shown below:

Replication starts by attaching tiles to any southeast, convex verticies.

The tiles keep growing around the shape until they make a rectangle.

A high level explanation of how shape replication in the signal passing tile assembly system works.

The next step is the actually replication. The only restriction on this process is that the shape to be replicated must be hole-free and the shape cannot have a choke-point anywhere of just one tile, i.e. it must have width of at least 2 at every point in the shape. Let P be a connected, hole-free, min-width 2 shape. The construction begins with designing a tile set that builds a frame around σ where dom (σ) = P which detaches upon completion by deactivating the glues of the signal passing tiles that connect them. Next, an inner ring forms within the completed ring. Once this ring within a ring is complete, it detaches and fills in its interior. The outer ring is then free to make another copy while the interior of the inner ring can host the growth of another frame. This means that the number of instances of the shape increases exponentially over time.