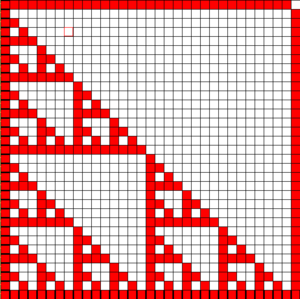
Self-Assembly of Fractals in the STAM
A method for assembling all discrete self-similar fractals in the STAM, and a specific example of a tile set for assembling the Sierpinski triangle.
Abstract
In this paper, we present high-level overviews of tile-based self-assembling systems capable of producing complex, infinite, aperiodic structures known as discrete self-similar fractals. Fractals have a variety of interesting mathematical and structural properties, and by utilizing the bottom-up growth paradigm of self-assembly to create them we not only learn important techniques for building such complex structures, we also gain insight into how similar structural complexity arises in natural self-assembling systems. Our results fundamentally leverage hierarchical assembly processes, and use as our building blocks square “tile” components which are capable of activating and de-activating their binding “glues” a constant number of times each, based only on local interactions. We provide the first constructions capable of building arbitrary discrete self-similar fractals at scale factor 1, and many at temperature 1 (i.e. “non-cooperatively”), including the Sierpinski triangle [1].
Overview
Fractals are mathematically interesting partially due to their complex self-similar structure. Fractals in nature often arrive at this structure through a series of local interactions motivated by simple rules; a process uniquely suited to simulation in self-assembly systems. The aTAM has been demonstrated to lack the ability to construct certain fractals and it is possible that the ATAM is unable to construct any non-trivial fractals. In previous work the 2HAM has been shown to have the ability to assemble general discrete self-similar fractals. In this paper the STAM, or signal-passing tile assembly model, is shown to have considerable powers in the assembly of discrete self-similar fractals. In particular, a tile set is demonstrated that can assemble the Sierpinski triangle at scale factor 1 and in temperature 1, and an algorithmic method for generating a tileset capable of assembling any discrete self-similar fractal at temperature 2 and an infinite subset at temperatue 1.
Results
The authors begin with a construction in the STAM that is capable of assembling the Sierpinski triangle at temperature 1 and scale factor 1.
The method begins with a set of hard-coded tiles, i.e. tiles that possess unique glues that only attach to one another, that build stage 2 Sierpinski triangle. Once a subassembly(stage n triangle) has completely assembled, one of a set of three initiator tiles binds to the new triagle and mark it as either a northern, western, or eastern triangle in the n+1 subassembly that it will join. Once a triangle has bonded with a particular initiator, it begins growing filler tiles that allow it to connect with other subassemblies of its stage. This process repeats at each stage infinitely and thus the Sierpinski triangle is assembled. The particulars of the explicit tile set are included in the paper [1].
The same essential ideas are used to design an algorithm that defines a tileset for any particular discrete self-similar fractal. As before, the construction begins with a hard-coded group of tiles for assembling the second stage of the assigned fractal. The remainder of the proof can be, to some extent, separated into the placement of special indicator glues at specific places on the subassemblies at each stage and the behaviors of filler glues that react to these indicators to order the subassemblies correctly in relation to one another. More information on these ideas is provided in the first paragraphs of section 6 and section 6.0.1, respectively [1].
In addition, the paper explains that the construction is valid for all discrete self-similar fractals at temperature 2, and with small modifications it is also valid for any discrete self-similar fractal which is singly-concave at temeperature 1. This is due to the particular behavior of the filler tiles that would allow for inappropriate binding of subassemblies at a different stage when the filler tiles are crossing a concavity at temperatue 1.
Further Work
The authors question whether the requirement that fractals be singly-concave may not be necessary at temperature 1, but note that a system without this requirement would necessitate extreme departures from the algorithm advanced in the paper. It is also possible that the 'junk' assemblies created by this method can be reduced in size. Lastly the authors suggest that their tile set for the Sierpinski triangle is nearly three times the size of a tile set that accomplishes the same goal but at scale factor 2, questioning if this size discrepancy can be reduced.