Covert Computation
Contents
Overview
Typically, algorithmic self-assembly leaves behind a permanent record of every step of the computation in the form of a final assembly. Analysis of this mass of tiles allows one to see every operation performed on the input as well as the input itself. In the modern world, sensitive data is rarely handled in this fashion since it would leave information vulnerable to theft by potential attackers. Covert computation in self-assembly should produce the correct output for a given computation while making it impossible to see the path the assembling process took to get there. The authors construct logic gates that satisfy these requirements in the growth-only (tiles are permanent once they attach) negative-glue aTAM[1].
Covert Circuits
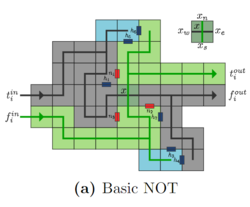
In order to conceal computational steps, the authors design logic gates in the aTAM that, after propagating their output signal, "backfill"[1]. Backfilling is the process of using tiles to fill in the unused input/output of the gate. For example, consider the NOT gate. If it receives a true input, it will output false to the next logical component. When the NOT gate backfills, the unused true output will begin to fill in all the way through to the false input. Below is their construction of the NOT gate and its two potential assembly paths. The true signal is generally the upper signal, while the false signal is lower. Solid lines denote strength 2 glues, and their arrows denote the direction of assembly. Blue glues are strength 1, and red glues are of strength -1, meaning they are repulsive.
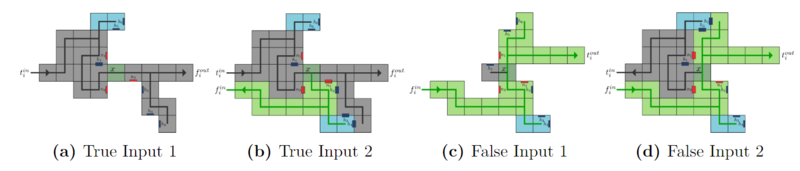
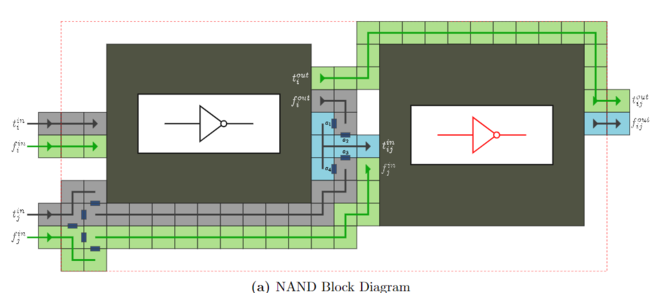
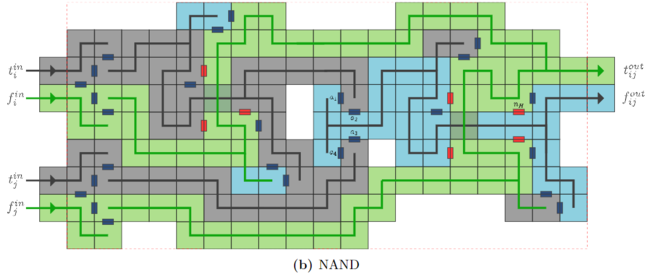
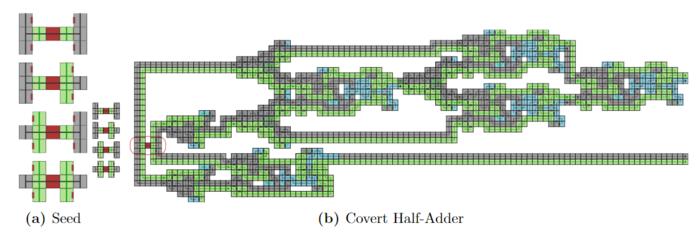
Using these covert NOT gates, it is possible to construct covert NAND gates as shown below. Finally, the authors show how to construct a covert half-adder but do not go further as the constructions become quite large. The half-adder is seeded (showed in the figure) such that extra tiles on the green portion represent a zero, and extra tiles on the gray represent a one. The left and right halves (separated by the red tile) are separate bits.
Results
The authors prove that their covert constructions can indeed compute any function computable by Boolean circuits by directly simulating Boolean circuits with their covert components [1]. They go on to prove that unique assembly verification in the growth-only negative-glue aTAM is coNP-complete by using their construction and a reduction from Planar Circuit SAT.