Concentration programming
aTAM progresses under the assumption that all reactants (tiles, assemblies, etc.) coexist in a test tube environment at equal and constant concentrations. Significant power may be added to the model if we allow variation in the form of tile concentration. Under normal conditions in the aTAM, assemblies only progress and grow via local interactions between glues on different tiles. Differing the global concentration of tiles in the test solution introduces another globally accessible information source.
Model Overview
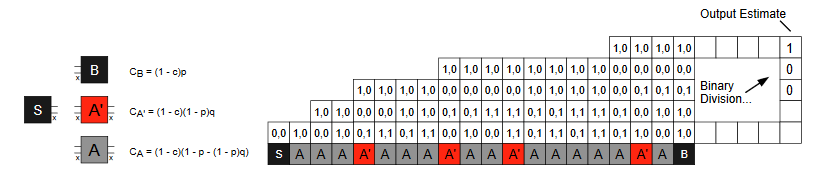
Introduced in [1], Tile Concentration Programming allows variable tile concentrations and thus the inclusion of additional information as input to a tile assembly system as the relative concentrations of the various tile types. These concentrations can be "sampled" by a static construction in a variant of aTAM which allows for a competitive binding race at specific locations on the construction. Multiple tile types may bind to these sampling slots, the final distribution of which serves as the assembly's "sample" of the environmental concentration distribution.
Results
Doty, in [2], showed the significant increase in power granted to aTAM systems by Concentration Programming. He showed that it is possible to construct (with arbitrarily high probability) nxn squares with a constant tile set, as well as scaled shapes where the concentration program and tile set depend on the shapes. The ability to vary concentration has also been demonstrated to decrease assembly time and the chance for errors [3], by Chen and Kao. Other results have shown the capability of this model to produce approximate [4] and exact [2] shapes with greatly reduced tile complexity and assembly time.
References
- ↑
Becker, Florent, Rapaport, Ivan, R{\'e}mila, Eric - Self-assemblying classes of shapes with a minimum number of tiles, and in optimal time
- International Conference on Foundations of Software Technology and Theoretical Computer Science pp. 45--56,2006
- BibtexAuthor : Becker, Florent, Rapaport, Ivan, R{\'e}mila, Eric
Title : Self-assemblying classes of shapes with a minimum number of tiles, and in optimal time
In : International Conference on Foundations of Software Technology and Theoretical Computer Science -
Address :
Date : 2006
- ↑ 2.0 2.1 2.2
Doty, David - Randomized self-assembly for exact shapes
- SIAM Journal on Computing 39(8):3521--3552,2010
- BibtexAuthor : Doty, David
Title : Randomized self-assembly for exact shapes
In : SIAM Journal on Computing -
Address :
Date : 2010
- ↑
Chen, Ho-Lin, Kao, Ming-Yang - Optimizing tile concentrations to minimize errors and time for DNA tile self-assembly systems
- International Workshop on DNA-Based Computers pp. 13--24,2010
- BibtexAuthor : Chen, Ho-Lin, Kao, Ming-Yang
Title : Optimizing tile concentrations to minimize errors and time for DNA tile self-assembly systems
In : International Workshop on DNA-Based Computers -
Address :
Date : 2010
- ↑
Kao, Ming-Yang, Schweller, Robert - Randomized self-assembly for approximate shapes
- International Colloquium on Automata, Languages, and Programming pp. 370--384,2008
- BibtexAuthor : Kao, Ming-Yang, Schweller, Robert
Title : Randomized self-assembly for approximate shapes
In : International Colloquium on Automata, Languages, and Programming -
Address :
Date : 2008