Two-Handed Assembly Model (2HAM)
The 2HAM [1] [2] is a generalization of the aTAM meant to model systems where self-assembly of multiple sub-assemblies can occur separately and in parallel, and then those sub-assemblies can combine with each other. The "2-handed" portion of the name comes from the fact that each combination is of exactly two assemblies at a time. Note that variations of this model have appeared in several papers and by several different names (e.g. hierarchical self-assembly, polyominoes, etc.) [3][4][1][5][6][7].
Contents
Informal Description of the Model
The 2HAM is formulated without a seed assembly structure, so that all individual tiles have equal status in the initial solution, and assembly begins as separate assemblies nucleate in parallel. Each step of assembly occurs as any two existing assemblies (which at first are just the singleton tiles) which are able to bind to each other, with strength at least equal to the temperature parameter and without any overlaps, combine to form a new assembly. Since it is experimentally challenging to enforce the seeded nature of growth in the aTAM (see kTAM), the 2HAM provides a perhaps more experimentally feasible model in that respect, by removing the seed constraint. However, since the 2HAM allows for pairs of arbitrarily large assemblies to combine with each other as long as there are no overlaps of any portions of those assemblies in the final configuration, two new difficulties arise in terms of experimental viability. First, the rate of diffusion of assemblies will decrease as their sizes increase, making it less and less likely for combinations of larger assemblies to occur. Second, in order to enforce the requirement that pairs of assemblies can only join in configurations in which they don't contain overlaps, it would need to be the case that assemblies are completely rigid (which is certainly not the case with DNA implementations of tiles) so that portions of the assemblies couldn't bend to avoid the overlaps. The fact that the 2HAM allows for the combination of arbitrarily large assemblies gives rise to the phenomenon that, although all interactions are local in the context of being between exactly two assemblies which are immediately adjacent to each other, there is also a notion of instantaneous long range interactions on the scale of individual tiles. This is because the existence of a tile at a location arbitrarily far from another can dictate whether or not that tile will be able to bind to a tile in another assembly by perhaps providing enough cooperative binding, or instead perhaps by blocking the assemblies from achieving a binding configuration. This long range interaction provides for a great amount of difference in the power of the 2HAM versus the aTAM, and is also the reason that the 2HAM isn't immediately similar to ACA systems (see Wang tiling vs. the aTAM).
Formal model definition
Two assemblies \(\alpha\) and \(\beta\) are disjoint if \(\dom \alpha \cap \dom \beta = \emptyset.\) For two assemblies \(\alpha\) and \(\beta\), define the union \(\alpha \cup \beta\) to be the assembly defined for all \(\vec{x}\in \mathbb{Z}^2\) by \((\alpha \cup \beta)(\vec{x}) = \alpha(\vec{x})\) if \(\alpha(\vec{x})\) is defined, and \((\alpha \cup \beta)(\vec{x}) = \beta(\vec{x})\) otherwise. Say that this union is disjoint if \(\alpha\) and \(\beta\) are disjoint.
The binding graph of an assembly \(\alpha\) is the grid graph \(G_\alpha = (V, E )\), where \(V = \dom{\alpha}\), and \(\{\vec{m}, \vec{n}\} \in E\) if and only if (1) \(\vec{m} - \vec{n} \in U_2\), (2) \(\lab_{\alpha(\vec{m})}\left(\vec{n} - \vec{m}\right) = \lab_{\alpha(\vec{n})}\left(\vec{m} - \vec{n}\right)\), and (3) \(\strength_{\alpha(\vec{m})}\left(\vec{n} -\vec{m}\right) > 0\). Given \(\tau \in \mathbb{N}\), an assembly is \(\tau\)-stable (or simply stable if \(\tau\) is understood from context), if it cannot be broken up into smaller assemblies without breaking bonds of total strength at least \(\tau\); i.e., if every cut of \(G_\alpha\) has weight at least \(\tau\), where the weight of an edge is the strength of the glue it represents. In contrast to the model of Wang tiling, the nonnegativity of the strength function implies that glue mismatches between adjacent tiles do not prevent a tile from binding to an assembly, so long as sufficient binding strength is received from the (other) sides of the tile at which the glues match.
For assemblies \(\alpha,\beta:\mathbb{Z}^2 \dashrightarrow T\) and \(\vec{u} \in \mathbb{Z}^2\), we write \(\alpha+\vec{u}\) to denote the assembly defined for all \(\vec{x}\in\mathbb{Z}^2\) by \((\alpha+\vec{u})(\vec{x}) = \alpha(\vec{x}-\vec{u})\), and write \(\alpha \simeq \beta\) if there exists \(\vec{u}\) such that \(\alpha + \vec{u} = \beta\); i.e., if \(\alpha\) is a translation of \(\beta\). Define the supertile of \(\alpha\) to be the set \(\tilde{\alpha} = \setr{\beta}{\alpha \simeq \beta}\). A supertile \(\tilde{\alpha}\) is \(\tau\)-stable (or simply stable) if all of the assemblies it contains are \(\tau\)-stable; equivalently, \(\tilde{\alpha}\) is stable if it contains a stable assembly, since translation preserves the property of stability. Note also that the notation \(|\tilde{\alpha}| \equiv |\alpha|\) is the size of the super tile (i.e., number of tiles in the supertile) is well-defined, since translation preserves cardinality (and note in particular that even though we define \(\tilde{\alpha}\) as a set, \(|\tilde{\alpha}|\) does not denote the cardinality of this set, which is always \(\aleph_0\)).
For two supertiles \(\tilde{\alpha}\) and \(\tilde{\beta}\), and temperature \(\tau\in\N\), define the combination set \(C^\tau_{\tilde{\alpha},\tilde{\beta}}\) to be the set of all supertiles \(\tilde{\gamma} \) such that there exist \(\alpha \in \tilde{\alpha}\) and \(\beta \in \tilde{\beta}\) such that (1) \(\alpha\) and \(\beta\) are disjoint (steric protection), (2) \(\gamma \equiv \alpha \cup \beta\) is \(\tau\)-stable, and (3) \(\gamma \in \tilde{\gamma} \). That is, \(C^\tau_{\tilde{\alpha},\tilde{\beta}}\) is the set of all \(\tau\)-stable supertiles that can be obtained by attaching \(\tilde{\alpha}\) to \(\tilde{\beta}\) stably, with \(|C^\tau_{\tilde{\alpha},\tilde{\beta}}| > 1\) if there is more than one position at which \(\beta\) could attach stably to \(\alpha\).
It is common with seeded assembly to stipulate an infinite number of copies of each tile, but our definition allows for a finite number of tiles as well. Our definition also allows for the growth of infinite assemblies and finite assemblies to be captured by a single definition, similar to the definitions of [8] for seeded assembly.
Given a set of tiles \(T\), define a state \(S\) of \(T\) to be a multiset of supertiles, or equivalently, \(S\) is a function mapping supertiles of \(T\) to \(\N \cup \{\infty\}\), indicating the multiplicity of each supertile in the state. We therefore write \(\tilde{\alpha} \in S\) if and only if \(S(\tilde{\alpha}) > 0\).
A (two-handed) tile assembly system (TAS) is an ordered triple \(\mathcal{T} = (T, S, \tau)\), where \(T\) is a finite set of tile types, \(S\) is the initial state, and \(\tau\in\N\) is the temperature. If not stated otherwise, assume that the initial state \(S\) is defined \(S(\tilde{\alpha}) = \infty\) for all \(\tilde{\alpha}\) such that \(|\tilde{\alpha}|=1\), and \(S(\tilde{\beta}) = 0\) for all other supertiles \(\tilde{\beta}\). That is, \(S\) is the state consisting of a countably infinite number of copies of each individual tile type from \(T\), and no other supertiles. In such a case we write \(\mathcal{T} = (T,\tau)\) to indicate that \(\mathcal{T}\) uses the default initial state.
Given a TAS \(\mathcal{T}=(T,S,\tau)\), define an assembly sequence of \(\mathcal{T}\) to be a sequence of states \(\vec{S} = (S_i \mid 0 \leq i < k)\) (where \(k = \infty\) if \(\vec{S}\) is an infinite assembly sequence), and \(S_{i+1}\) is constrained based on \(S_i\) in the following way: There exist supertiles \(\tilde{\alpha},\tilde{\beta},\tilde{\gamma} \) such that (1) \(\tilde{\gamma}\in C^\tau_{\tilde{\alpha},\tilde{\beta}}\), (2) \(S_{i+1}(\tilde{\gamma}) = S_{i}(\tilde{\gamma}) + 1\),with the convention that \(\infty = \infty + 1 = \infty - 1\) (3) if \(\tilde{\alpha} \neq \tilde{\beta}\), then \(S_{i+1}(\tilde{\alpha}) = S_{i}(\tilde{\alpha}) - 1\), \(S_{i+1}(\tilde{\beta}) = S_{i}(\tilde{\beta}) - 1\), otherwise if \(\tilde{\alpha} = \tilde{\beta}\), then \(S_{i+1}(\tilde{\alpha}) = S_{i}(\tilde{\alpha}) - 2\), and (4) \(S_{i+1}(\tilde{\omega}) = S_{i}(\tilde{\omega})\) for all \(\tilde{\omega} \not\in \{\tilde{\alpha},\tilde{\beta},\tilde{\gamma} \}\). That is, \(S_{i+1}\) is obtained from \(S_i\) by picking two supertiles from \(S_i\) that can attach to each other, and attaching them, thereby decreasing the count of the two reactant supertiles and increasing the count of the product supertile. If \(S_0 = S\), we say that \(\vec{S}\) is nascent.
Unlike the seeded model, an infinite assembly sequence in the two-handed model may not have a unique limit state. For example, consider an assembly sequence that starts from an infinite number of single tiles, then continually creates a size-2 supertile \(\tilde{\alpha}\) from tiles before attaching \(\tilde{\alpha}\) to a larger and ever-growing supertile. The count of \(\tilde{\alpha}\) forever oscillates between 0 and 1, so there is no limit state, although the larger supertile, which is more precisely a sequence of supertiles, will have a well-defined limit.
Given an assembly sequence \(\vec{S} = (S_i \mid 0 \leq i < k)\) of \(\mathcal{T}=(T,S,\tau)\) and a supertile \(\tilde{\gamma} \in S_i\) for some \(i\), define the predecessors of \(\tilde{\gamma}\) in \(\vec{S}\) to be the multiset \(\mathrm{pred}_{\vec{S}}(\tilde{\gamma}) = \{\tilde{\alpha},\tilde{\beta}\}\) if \(\tilde{\alpha},\tilde{\beta} \in S_{i-1}\) and \(\tilde{\alpha}\) and \(\tilde{\beta}\) attached to create \(\tilde{\gamma}\) at step \(i\) of the assembly sequence, and define \(\mathrm{pred}_{\vec{S}}(\tilde{\gamma}) = \{ \tilde{\gamma} \}\) otherwise. Define the successor of \(\tilde{\gamma}\) in \(\vec{S}\) to be \(\mathrm{succ}_{\vec{S}}(\tilde{\gamma})=\tilde{\alpha}\) \(\tilde{\gamma}\) is a predecessor of \(\tilde{\alpha}\) in \(\vec{S}\), and define \(\mathrm{succ}_{\vec{S}}(\tilde{\gamma})=\tilde{\gamma}\) otherwise. A sequence of supertiles \(\vec{\tilde{\alpha}} = (\tilde{\alpha}_i \mid 0 \leq i < k)\) is a supertile assembly sequence of \(\mathcal{T}\) if there is an assembly sequence \(\vec{S} = (S_i \mid 0 \leq i < k)\) of \(\mathcal{T}\) such that, for all \(1 \leq i < k\), \(\mathrm{succ}_{\vec{S}}(\tilde{\alpha}_{i-1}) = \tilde{\alpha}_i\), and \(\vec{\tilde{\alpha}}\) is nascent if \(\vec{S}\) is nascent.
The result of a supertile assembly sequence \(\vec{\tilde{\alpha}}\) is the unique supertile \(\res{\vec{\tilde{\alpha}}}\) such that there exist an assembly \(\alpha \in \res{\vec{\tilde{\alpha}}}\) and, for each \(0 \leq i < k\), assemblies \(\alpha_i \in \tilde{\alpha}_i\) such that \(\dom{\alpha} = \bigcup_{0 \leq i < k}{\dom{\alpha_i}}\) and, for each \(0 \leq i < k\), \(\alpha_i \sqsubseteq \alpha\). For all supertiles \(\tilde{\alpha},\tilde{\beta}\), we write \(\tilde{\alpha} \to_\mathcal{T} \tilde{\beta}\) (or \(\tilde{\alpha} \to \tilde{\beta}\) when \(\mathcal{T}\) is clear from context) to denote that there is a supertile assembly sequence \(\vec{\tilde{\alpha}} = ( \tilde{\alpha}_i \mid 0 \leq i < k )\) such that \(\tilde{\alpha}_0 = \tilde{\alpha}\) and \(\res{\vec{\tilde{\alpha}}} = \tilde{\beta}\). It can be shown using the techniques of [9] for seeded systems that for all two-handed tile assembly systems \(\mathcal{T}\) supplying an infinite number of each tile type, \(\to_\mathcal{T}\) is a transitive, reflexive relation on supertiles of \(\mathcal{T}\). We write \(\tilde{\alpha} \to_\mathcal{T}^1 \tilde{\beta}\) (\(\tilde{\alpha} \to^1 \tilde{\beta}\)) to denote an assembly sequence of length 1 from \(\tilde{\alpha}\) to \(\tilde{\beta}\) and \(\tilde{\alpha} \to_\mathcal{T}^{\leq 1} \tilde{\beta}\) (\(\tilde{\alpha} \to^{\leq 1} \tilde{\beta}\)) to denote an assembly sequence of length 1 from \(\tilde{\alpha}\) to \(\tilde{\beta}\) if \(\tilde{\alpha} \ne \tilde{\beta}\), and otherwise (i.e. \(\tilde{\alpha} = \tilde{\beta}\)) an assembly sequence of length 0.
A supertile \(\tilde{\alpha}\) is producible, and we write \(\tilde{\alpha} \in \mathcal{A}[\mathcal{\mathcal{T}}]\), if it is the result of a nascent supertile assembly sequence. A supertile \(\tilde{\alpha}\) is terminal if, for all producible supertiles \(\tilde{\beta}\), \(C^\tau_{\tilde{\alpha},\tilde{\beta}} = \emptyset\). Note that a supertile \(\tilde{\alpha}\) could be non-terminal in the sense that there is a producible supertile \(\tilde{\beta}\) such that \(C^\tau_{\tilde{\alpha},\tilde{\beta}} \neq \emptyset\), yet it may not be possible to produce \(\tilde{\alpha}\) and \(\tilde{\beta}\) simultaneously if some tile types are given finite initial counts, implying that \(\tilde{\alpha}\) cannot be "grown" despite being non-terminal. If the count of each tile type in the initial state is \(\infty\), then all producible supertiles are producible from any state, and the concept of terminal becomes synonymous with "not able to grow", since it would always be possible to use the abundant supply of tiles to assemble \(\tilde{\beta}\) alongside \(\tilde{\alpha}\) and then attach them.} Define \(\mathcal{A}_{\Box}[\mathcal{\mathcal{T}}] \subseteq \mathcal{A}[\mathcal{\mathcal{T}}]\) to be the set of terminal and producible supertiles of \(\mathcal{T}\). \(\mathcal{T}\) is directed (a.k.a., deterministic, confluent) if \(|\mathcal{A}_{\Box}[\mathcal{\mathcal{T}}]| = 1\).
Let \(X \subseteq \mathbb{Z}^2\) be a shape. We say \(X\) self-assembles in \(\mathcal{T}\) if, for each \(\tilde{\alpha} \in \mathcal{A}_{\Box}[\mathcal{\mathcal{T}}]\), there exists \(\alpha \in \tilde{\alpha}\) such that \(\dom \alpha = X\); i.e., \(\mathcal{T}\) uniquely assembles into the shape \(X\).
Example
In this section we provide an example of a simple 2HAM system and show exactly what assemblies are producible within it in order to help clarify the ways in which assemblies are produced within the model.
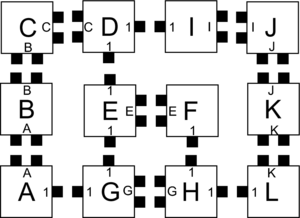
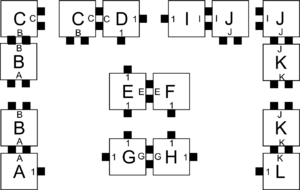
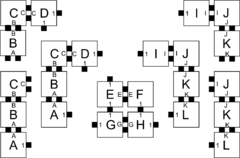
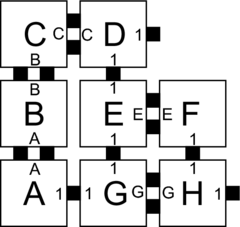
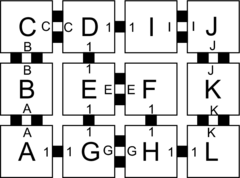
Let \(\mathcal{T} = (T,2)\) be a 2HAM system where \(T\) is defined as the tile types in Figure 1. Figures 1-5 show the complete set of 29 supertiles which make up \(\mathcal{A}[\mathcal{T}]\), and Figure 5 shows the single member of \(\mathcal{A}_{\Box}[\mathcal{T}]\). The producible supertiles are broken into groups to show the earliest step of combinations during which they can appear, although for some there are multiple paths of combinations which can form them. (We don't show duplicate copies.) Furthermore, recall from the definition of the model that all producible supertiles are available at every step, so for example a supertile produced in step 2 may combine with one produced in step 1 to create a new supertile in step 3. Also note that the use of "steps" is merely a convenience for discussing this example, but typically the sets \(\mathcal{A}[\mathcal{T}]\) and \(\mathcal{A}_{\Box}[\mathcal{T}]\) are simply defined as those supertiles producible in the limit.In this section we provide an example of a simple 2HAM system and show exactly what assemblies are producible within it in order to help clarify the ways in which assemblies are produced within the model.
2HAM Results
Intrinsic Universality in the 2HAM
Impossibility and Efficiency Comparisions Between aTAM and 2HAM
Fuzzy Temperature Fault Tolerance
References
- ↑ 1.0 1.1
Qi Cheng, Gagan Aggarwal, Michael H. Goldwasser, Ming-Yang Kao, Robert T. Schweller, Pablo Moisset de Espanés - Complexities for Generalized Models of Self-Assembly
- ↑
Erik D. Demaine, Martin L. Demaine, Sándor P. Fekete, Mashhood Ishaque, Eynat Rafalin, Robert T. Schweller, Diane L. Souvaine - Staged self-assembly: nanomanufacture of arbitrary shapes
with O(1) glues
- Natural Computing 7(3):347-370,2008
- BibtexAuthor : Erik D. Demaine, Martin L. Demaine, Sándor P. Fekete, Mashhood Ishaque, Eynat Rafalin, Robert T. Schweller, Diane L. Souvaine
Title : Staged self-assembly: nanomanufacture of arbitrary shapes with O(1) glues
In : Natural Computing -
Address :
Date : 2008
- ↑
Erik Winfree - Self-healing Tile Sets
- Nanotechnology: Science and Computation pp. 55--78,2006
- http://dx.doi.org/10.1007/3-540-30296-4_4
BibtexAuthor : Erik Winfree
Title : Self-healing Tile Sets
In : Nanotechnology: Science and Computation -
Address :
Date : 2006
- ↑
Ho-Lin Chen, Ashish Goel, Chris Luhrs - Dimension augmentation and combinatorial criteria for efficient error-resistant DNA self-assembly
- Proceedings of the nineteenth annual ACM-SIAM symposium on Discrete algorithms pp. 409--418, Philadelphia, PA, USA,2008
- BibtexAuthor : Ho-Lin Chen, Ashish Goel, Chris Luhrs
Title : Dimension augmentation and combinatorial criteria for efficient error-resistant DNA self-assembly
In : Proceedings of the nineteenth annual ACM-SIAM symposium on Discrete algorithms -
Address : Philadelphia, PA, USA
Date : 2008
- ↑
Demaine, ErikD., Eisenstat, Sarah, Ishaque, Mashhood, Winslow, Andrew - One-dimensional staged self-assembly
- ↑
Leonard Adleman, Qi Cheng, Ashish Goel, Ming-Deh Huang, Hal Wasserman - Linear Self-Assemblies: Equilibria, Entropy and Convergence Rates
- In Sixth International Conference on Difference Equations and Applications ,2001
- BibtexAuthor : Leonard Adleman, Qi Cheng, Ashish Goel, Ming-Deh Huang, Hal Wasserman
Title : Linear Self-Assemblies: Equilibria, Entropy and Convergence Rates
In : In Sixth International Conference on Difference Equations and Applications -
Address :
Date : 2001
- ↑
Leonard Adleman - Toward a Mathematical Theory of Self-Assembly
(Extended Abstract)
- Technical Report, University of Southern California (00-722),2000
- http://citeseer.ist.psu.edu/272447.html;
ftp://ftp.usc.edu/pub/csinfo/tech-reports/papers/00-722.ps.Z
BibtexAuthor : Leonard Adleman
Title : Toward a Mathematical Theory of Self-Assembly (Extended Abstract)
In : Technical Report, University of Southern California -
Address :
Date : 2000
- ↑
James I. Lathrop, Jack H. Lutz, Scott M. Summers - Strict Self-Assembly of Discrete Sierpinski Triangles
- Theoretical Computer Science 410:384--405,2009
- BibtexAuthor : James I. Lathrop, Jack H. Lutz, Scott M. Summers
Title : Strict Self-Assembly of Discrete Sierpinski Triangles
In : Theoretical Computer Science -
Address :
Date : 2009
- ↑
Paul W. K. Rothemund - Theory and Experiments in Algorithmic Self-Assembly
- Ph.D. Thesis, University of Southern California , December 2001
- BibtexAuthor : Paul W. K. Rothemund
Title : Theory and Experiments in Algorithmic Self-Assembly
In : Ph.D. Thesis, University of Southern California -
Address :
Date : December 2001