Difference between revisions of "Simulation in the aTAM"
Jhendricks (talk | contribs) (→Example) |
Jhendricks (talk | contribs) (→Example) |
||
| Line 18: | Line 18: | ||
| alt3 = A tile set that simulates single tile line assembly | | alt3 = A tile set that simulates single tile line assembly | ||
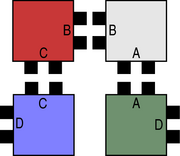
| caption3 = We can see that each tile of labeled $L$ is represented by some $2\times 2$ block. | | caption3 = We can see that each tile of labeled $L$ is represented by some $2\times 2$ block. | ||
| + | | width3 = 360px | ||
}} | }} | ||
Revision as of 16:10, 12 July 2013
Contents
Informal Description of Simulation
For TAS's \(\mathcal{T}\) and \(\mathcal{S}\), simulation of \(\mathcal{T}\) by \(\mathcal{S}\) can be done according to a simple "block substitution scheme" where equal-size square blocks of tiles in assemblies produced by \(\mathcal{S}\) represent tiles in assemblies produced by \(\mathcal{T}\). Furthermore, since we wish to simulate the entire process of self-assembly, and not only the final result, it is critical that the simulation be such that the "local transition rules" involving intermediate producible (and nonterminal) assemblies of \(\mathcal{T}\) be faithfully represented in the simulation.
Example
A single tile that assembles a line can be simulation in such a way that each tile of the simulated line is represented by \(2\times 2\) blocks.
Formal Definition
Preliminaries
From this point on, let \(T\) be a \(d\)-dimensional tile set, and let \(m\in\mathbb{Z}^+\). An \(m\)-block supertile over \(T\) is a partial function \(\alpha:\mathbb{Z}_m^d \dashrightarrow T\), where \(\mathbb{Z}_m = \{0,1,\ldots,m-1\}\). Note that the dimension of the \(m\)-block is implicitly defined by the dimension of \(T\). Let \(B^T_m\) be the set of all \(m\)-block supertiles over \(T\). The \(m\)-block with no domain is said to be empty. For a general assembly \(\alpha:\mathbb{Z}^d \dashrightarrow T\) and \((x_0,\ldots x_{d-1})\in\mathbb{Z}^d\), define \(\alpha^m_{x_0,\ldots x_{d-1}}\) to be the \(m\)-block supertile defined by \(\alpha^m_{x_0,\ldots, x_{d-1}}(i_0,\ldots, i_{d-1}) = \alpha(mx_0+i_0,\ldots, mx_{d-1}+i_{d-1})\) for \(0 \leq i_0, \ldots, i_{d-1}< m.\) For some tile set \(S\) of dimension \(d' \geq d\), a partial function \(R: B^{S}_m \dashrightarrow T\) is said to be a valid \(m\)-block supertile representation from \(S\) to \(T\) if for any \(\alpha,\beta \in B^{S}_m\) such that \(\alpha \sqsubseteq \beta\) and \(\alpha \in \dom R\), then \(R(\alpha) = R(\beta)\).
Let \(d' \in \{ 2,3 \}\) and \(d \in \{ d' -1, d' \} \). Let \(f: \mathbb{Z}^{d'} \rightarrow \mathbb{Z}^{d}\), where \(f(x_0,\ldots,x_{d'-1}) = (x_0,\ldots,x_{d'-1})\) if \(d'=d\) and \(f(x_0,\ldots,x_{d'-1}) = (x_0,\ldots,x_{d-1},0)\) if \(d = d' -1\), and undefined otherwise. For a given valid \(m\)-block supertile representation function \(R\) from tile set \(S\) to tile set \(T\), define the assembly representation function \(R^*: \mathcal{A}^{S} \rightarrow \mathcal{A}^T\) such that \(R^*(\alpha') = \alpha\) if and only if \(\alpha(x_0,\ldots, x_{d-1}) = R\left(\alpha'^m_{x_0,\ldots, x_{d'-1}}\right)\) for all \((x_0,\ldots x_{d'-1}) \in \Z^{d'-1}\). Note that \(R^*\) is a total function since every assembly of \(S\) represents some assembly of \(T\); the functions \(R\) and \(\alpha\) are partial to allow undefined points to represent empty space. For an assembly \(\alpha' \in \mathcal{A}^{S}\) such that \(R(\alpha') = \alpha\), \(\alpha'\) is said to map cleanly to \(\alpha \in \mathcal{A}^T\) under \(R^*\) if for all non empty blocks \(\alpha'^m_{x_0,\ldots, x_{d'-1}},\) \((f(x_0,\ldots,x_{d'-1})+f(u_0,\ldots,u_{d'-1})) \in \dom \alpha\) for some \(u_0,\ldots, u_{d'-1} \in \{-1,0,1\}\) such that \(u_0^2 + \cdots + u_{d'-1}^2 \leq 1\), or if \(\alpha'\) has at most one non-empty \(m\)-block \(\alpha^m_{0, \ldots, 0}\). In other words, \(\alpha'\) may have tiles on supertile blocks representing empty space in \(\alpha\), but only if that position is adjacent to a tile in \(\alpha\). We call such growth "around the edges" of \(\alpha'\) fuzz and thus restrict it to be adjacent to only valid supertiles, but not diagonally adjacent (i.e. we do not permit diagonal fuzz).
In the following definitions, let \(\mathcal{T} = \left(T,\sigma_T,\tau_T\right)\) be a \(d\)-TAS for \(d \in \{2,3\}\), let \(\mathcal{S} = \left(S,\sigma_S,\tau_S\right)\) be a \(d'\)-TAS for \(d' \geq d\), and let \(R\) be an \(m\)-block representation function \(R:B^S_m \rightarrow T\).
Equivalent production
We say that \(\mathcal{S}\) and \(\mathcal{T}\) have equivalent productions (under \(R\)), and we write \(\mathcal{S} \Leftrightarrow \mathcal{T}\) if the following conditions hold:
- \(\left\{R^*(\alpha') | \alpha' \in \prodasm{\mathcal{S}}\right\} = \prodasm{\mathcal{T}}\).
- \(\left\{R^*(\alpha') | \alpha' \in \termasm{\mathcal{S}}\right\} = \termasm{\mathcal{T}}\).
- For all \(\alpha'\in \prodasm{\mathcal{S}}\), \(\alpha'\) maps cleanly to \(R^*(\alpha')\).
Equivalent dynamics
Follows
We say that \(\mathcal{T}\) follows \(\mathcal{S}\) (under \(R\)), and we write \(\mathcal{T} \dashv_R \mathcal{S}\) if \(\alpha' \rightarrow^\mathcal{S} \beta'\), for some \(\alpha',\beta' \in \mathcal{A}[\mathcal{S}]\), implies that \(R^*(\alpha') \to^\mathcal{T} R^*(\beta')\).
Models
We say that \(\mathcal{S}\) models \(\mathcal{T}\) (under \(R\)), and we write \(\mathcal{S} \models_R \mathcal{T}\), if for every \(\alpha \in \mathcal{A}[\mathcal{T}]\), there exists \(\Pi \subset \mathcal{A}[\mathcal{S}]\) where \(R^*(\alpha') = \alpha\) for all \(\alpha' \in \Pi\), such that, for every \(\beta \in \mathcal{A}[\mathcal{T}]\) where \(\alpha \rightarrow^\mathcal{T} \beta\), (1) for every \(\alpha' \in \Pi\) there exists \(\beta' \in \mathcal{A}[\mathcal{S}]\) where \(R^*(\beta') = \beta\) and \(\alpha' \rightarrow^\mathcal{S} \beta'\), and (2) for every \(\alpha'' \in \mathcal{A}[\mathcal{S}]\) where \(\alpha'' \rightarrow^\mathcal{S} \beta'\), \(\beta' \in \mathcal{A}[\mathcal{S}]\), \(R^*(\alpha'') = \alpha\), and \(R^*(\beta') = \beta\), there exists \(\alpha' \in \Pi\) such that \(\alpha' \rightarrow^\mathcal{S} \alpha''\).
The previous definition essentially specifies that every time \(\mathcal{S}\) simulates an assembly \(\alpha \in \mathcal{A}[\mathcal{T}]\), there must be at least one valid growth path in \(\mathcal{S}\) for each of the possible next steps that \(\mathcal{T}\) could make from \(\alpha\) which results in an assembly in \(\mathcal{S}\) that maps to that next step.
Simulation
We say that \(\mathcal{S}\) simulates \(\mathcal{T}\) (under \(R\)) if \(\mathcal{S} \Leftrightarrow_R \mathcal{T}\) (equivalent productions), \(\mathcal{T} \dashv_R \mathcal{S}\) and \(\mathcal{S} \models_R \mathcal{T}\) (equivalent dynamics).