Difference between revisions of "Oritatami"
| (21 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
RNA is generated by the following process: | RNA is generated by the following process: | ||
| + | |||
| + | [[File:rna_origami_small.bmp|thumb|right|RNA transcription.]] | ||
1. The enzyme RNAP (RNA polymerase) unzips a double-stranded DNA helix. | 1. The enzyme RNAP (RNA polymerase) unzips a double-stranded DNA helix. | ||
| + | |||
2. RNAP attaches to one of the unzipped strands at a promoting sequence of nucleotides. | 2. RNAP attaches to one of the unzipped strands at a promoting sequence of nucleotides. | ||
| + | |||
3. RNAP travels linearly along the DNA strand from the promoter sequence, reading the DNA's nucleotides. As it does so, it adds the complementary ribonucleotides to the RNA strand growing out of it. | 3. RNAP travels linearly along the DNA strand from the promoter sequence, reading the DNA's nucleotides. As it does so, it adds the complementary ribonucleotides to the RNA strand growing out of it. | ||
| + | |||
4. RNAP releases the grown RNA strand upon reading a terminating sequence of nucleotides. | 4. RNAP releases the grown RNA strand upon reading a terminating sequence of nucleotides. | ||
| − | Cotranscriptional folding occurs as the | + | Cotranscriptional folding occurs ''as'' the RNA strand is elongated. In other words, hydrogen bonds form between ribonucleotides in the strand as new ones are added to it, not afterword. Hence, the form of the strand at the time of its release is not simply that which has the minimum energy. Rather, it is the one which has "stepwise" minimum energy. At any point in time only the last few ribonucleotides in the sequence may rearrange themselves; the rest must preserve their existing bonds. |
| + | |||
| + | ==Oritatami Systems== | ||
| + | |||
| + | Oritatami systems (OSs) formalize the cotranscriptional folding from a DNA transcript by the following model: | ||
| + | |||
| + | An OS $\mathcal{O}$ is a triple $\left(b, \circ, \delta\right)$ where: | ||
| − | + | 1. $b$ is sequence of bead types $\left(b_i \in B\right)$ taken from a finite alphabet $B$. $b$ is $\mathcal{O}$'s transcript; it is a formalization of the DNA transcript in RNA transcription. The "beads" may represent single ribonucleotides or sequences of ribonucleotides. In the model they are simply "bonding elements". | |
| − | + | 2. $\circ \subset B^2$ is a symmetric binary relation on $\mathcal{O}$'s bead types. $\circ$ determines which beads may bond with one another. | |
| − | + | 3. $\delta$ is the system's delay. $\delta$ gives the number of beads at the end of the system's configuration which may rearrange themselves at each time step. $\delta$ is determined in implementation by RNAP's transcription rate. If RNAP transcribes very quickly, only the most recent ribonucleotide added to the RNA strand will be able to rearrange itself. If RNAP transcribes very slowly, much of the strand will rearrange itself between additions. | |
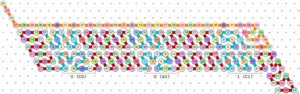
| − | + | [[File:oritatami_counter.png|thumb|right|Sample OS configuration, binary counter.]] | |
| − | |||
| − | |||
| − | + | $\mathcal{O}$'s state is a configuration of beads. Here a "configuration" is a laying out of a sequence of beads self-avoidingly within the plane. More formally: | |
| − | + | Let $\mathbb{T} = \left(\mathbb{Z}^2, \sim\right)$ where $A \sim B$ if and only if $\left|A-B\right| \in \left\{(0,1), (1,0), (1,1)\right\}$. $\mathbb{T}$ is then a triangular lattice over the plane. | |
| + | Let $\left(w_i \in B\right)$ be a sequence of beads. Assign each $w_i$ to a point $X_i$ in $\mathbb{Z}^2$ such that $X_i \sim X_{i+1}$ for all $w_i$. Moreover, assign points to the beads in such a way that no distinct $w_i$ and $w_j$ have the same point. The resulting assignation is a valid configuration of the bead sequence $\left(w_i\right)$. I will refer to a configuration as a sequence $\left(c_i \in B \times \mathbb{Z}^2\right)$, where $c_i\circ c_j$ if and only if the contained bead types $w_i \circ w_j$ and the contained positions $X_i \sim X_j$. In other words, two beads in a configuration are related to one another if they are adjacent and bondable. | ||
| + | Let $C=\left(c_i\right)$ be a configuration of an OS $\mathcal{O}$. | ||
| − | + | \[ | |
| − | + | e(c_i)=\sum_{i > j+1}{\begin{cases}-1 & c_i \circ c_j \\ 0 & \text{otherwise}\end{cases}} | |
| − | + | \] | |
| + | \[ | ||
| + | E(C=\left(c_i\right)) = \sum_{c_i}{e(c_i)} | ||
| − | + | \] | |
| + | $E$ counts the bonds in a configuration. Bonds are given negative value because they reduce the energy of the system. | ||
| + | Let $S_n=\left\{C_i\right\}$ be a set of configurations of the first $n$ beads in $\mathcal{O}$'s transcript $b$. Let $C^{\leftarrow k}$ be the configuration obtained by removing the last $k$ beads in $C$. Let $C^{\rightarrow k}$ be the set of configurations obtainable by adding the next $k$ beads in the transcript to $C$. $S^{\leftarrow k}=\{C^{\leftarrow k} | C \in S\}$ and $S^{\rightarrow k}=\{X | X \in C^{\rightarrow k} \in S\}$. | ||
| + | An update $H(S_n)$ on $S_n$ is given by: | ||
| + | |||
| + | \[ | ||
| + | H(S_n)=\begin{cases} \texttt{argmin }H\left(()^{\rightarrow n+1}\right) & n < \delta-1 \\ | ||
| + | |||
| + | \bigcup_{\gamma \in S^{\leftarrow \delta-1}}{\texttt{argmin }H\left(\gamma^{\rightarrow \delta}\right)} & n \geq \delta-1 | ||
| + | \end{cases} | ||
| + | |||
| + | \] | ||
| + | |||
| + | In other words, updating a set of configurations of a subsequence of the transcript replaces each configuration with the set of configurations with one more bead from the transcript and minimum energy in the last $\delta$ beads. | ||
| + | |||
| + | The set of possible end states of $\mathcal{O}$ is given by $H^n(\left\{()\right\})$, where $n$ is the length of the transcript and $()$ is an empty configuration. | ||
| + | |||
| + | Further consideration of the model is given by Geary, Meunier, Schabanel and Seki<ref name=ori_intro/>. | ||
==Turing-Completeness== | ==Turing-Completeness== | ||
| − | Given the history-dependent nature of the RNA strand's energy level, it is reasonalbe to guess that the oritatami model permits Turing-complete computation. Indeed, this has been confirmed by Geary, Meunier, | + | Given the history-dependent nature of the RNA strand's energy level, it is reasonalbe to guess that the oritatami model permits Turing-complete computation. Indeed, this has been confirmed by Geary, Meunier, Schabanel and Seki, whose paper<ref name=ori_turing/> showed that the oritatami model permits Turing-complete computation subject to only polynomial inflation in input size. This was shown as follows: |
\[ | \[ | ||
| Line 51: | Line 81: | ||
==Shape-Folding== | ==Shape-Folding== | ||
| − | + | Demaine et. al.<ref name=ori_shape/> have shown the following. There are shapes which unfoldable by all OSs. It is NP-hard to answer the general question "Is this shape foldable by an OS?" However, it has been shown that every shape inflated 3 times is foldable by an OS with delay 1. Moreover, every shape inflated 2 times is foldable by an OS with some finite delay delta. In general, for any OS with delay $\delta>2$, there are shapes which it can fold but which it cannot fold for any smaller delay $\delta' < \delta$. | |
| + | ==References== | ||
| + | <references> | ||
| − | = | + | <ref name="ori_turing"> |
<bibtex> | <bibtex> | ||
@misc{geary2015proving, | @misc{geary2015proving, | ||
| Line 64: | Line 96: | ||
archivePrefix={arXiv}, | archivePrefix={arXiv}, | ||
primaryClass={cs.CG} | primaryClass={cs.CG} | ||
| − | } | + | }</bibtex></ref> |
| + | <ref name="ori_shape"> | ||
| + | <bibtex> | ||
@misc{demaine2018know, | @misc{demaine2018know, | ||
title={Know When to Fold 'Em: Self-Assembly of Shapes by Folding in Oritatami}, | title={Know When to Fold 'Em: Self-Assembly of Shapes by Folding in Oritatami}, | ||
| Line 74: | Line 108: | ||
primaryClass={cs.DS} | primaryClass={cs.DS} | ||
} | } | ||
| + | </bibtex> | ||
| + | </ref> | ||
| + | |||
| + | <ref name="ori_intro"> | ||
| + | <bibtex> | ||
| + | @article{Geary_2019, title={Oritatami: A Computational Model for Molecular Co-Transcriptional Folding}, volume={20}, ISSN={1422-0067}, url={http://dx.doi.org/10.3390/ijms20092259}, DOI={10.3390/ijms20092259}, number={9}, journal={International Journal of Molecular Sciences}, publisher={MDPI AG}, author={Geary, Cody and Meunier, Pierre-Étienne and Schabanel, Nicolas and Seki, Shinnosuke}, year={2019}, month={May}, pages={2259}} | ||
| + | </bibtex> | ||
| + | </ref> | ||
| − | + | </references> | |
| − | + | ||
| − | + | [[Category:self-assembly]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 09:14, 23 July 2020
Oritatami (折りたたみ, "folding") is a mathematical model describing cotranscriptional RNA folding.
Contents
Cotranscriptional RNA Folding
RNA is generated by the following process:
1. The enzyme RNAP (RNA polymerase) unzips a double-stranded DNA helix.
2. RNAP attaches to one of the unzipped strands at a promoting sequence of nucleotides.
3. RNAP travels linearly along the DNA strand from the promoter sequence, reading the DNA's nucleotides. As it does so, it adds the complementary ribonucleotides to the RNA strand growing out of it.
4. RNAP releases the grown RNA strand upon reading a terminating sequence of nucleotides.
Cotranscriptional folding occurs as the RNA strand is elongated. In other words, hydrogen bonds form between ribonucleotides in the strand as new ones are added to it, not afterword. Hence, the form of the strand at the time of its release is not simply that which has the minimum energy. Rather, it is the one which has "stepwise" minimum energy. At any point in time only the last few ribonucleotides in the sequence may rearrange themselves; the rest must preserve their existing bonds.
Oritatami Systems
Oritatami systems (OSs) formalize the cotranscriptional folding from a DNA transcript by the following model:
An OS \(\mathcal{O}\) is a triple \(\left(b, \circ, \delta\right)\) where:
1. \(b\) is sequence of bead types \(\left(b_i \in B\right)\) taken from a finite alphabet \(B\). \(b\) is \(\mathcal{O}\)'s transcript; it is a formalization of the DNA transcript in RNA transcription. The "beads" may represent single ribonucleotides or sequences of ribonucleotides. In the model they are simply "bonding elements".
2. \(\circ \subset B^2\) is a symmetric binary relation on \(\mathcal{O}\)'s bead types. \(\circ\) determines which beads may bond with one another.
3. \(\delta\) is the system's delay. \(\delta\) gives the number of beads at the end of the system's configuration which may rearrange themselves at each time step. \(\delta\) is determined in implementation by RNAP's transcription rate. If RNAP transcribes very quickly, only the most recent ribonucleotide added to the RNA strand will be able to rearrange itself. If RNAP transcribes very slowly, much of the strand will rearrange itself between additions.
\(\mathcal{O}\)'s state is a configuration of beads. Here a "configuration" is a laying out of a sequence of beads self-avoidingly within the plane. More formally:
Let \(\mathbb{T} = \left(\mathbb{Z}^2, \sim\right)\) where \(A \sim B\) if and only if \(\left|A-B\right| \in \left\{(0,1), (1,0), (1,1)\right\}\). \(\mathbb{T}\) is then a triangular lattice over the plane.
Let \(\left(w_i \in B\right)\) be a sequence of beads. Assign each \(w_i\) to a point \(X_i\) in \(\mathbb{Z}^2\) such that \(X_i \sim X_{i+1}\) for all \(w_i\). Moreover, assign points to the beads in such a way that no distinct \(w_i\) and \(w_j\) have the same point. The resulting assignation is a valid configuration of the bead sequence \(\left(w_i\right)\). I will refer to a configuration as a sequence \(\left(c_i \in B \times \mathbb{Z}^2\right)\), where \(c_i\circ c_j\) if and only if the contained bead types \(w_i \circ w_j\) and the contained positions \(X_i \sim X_j\). In other words, two beads in a configuration are related to one another if they are adjacent and bondable.
Let \(C=\left(c_i\right)\) be a configuration of an OS \(\mathcal{O}\).
\[ e(c_i)=\sum_{i > j+1}{\begin{cases}-1 & c_i \circ c_j \\ 0 & \text{otherwise}\end{cases}} \] \[ E(C=\left(c_i\right)) = \sum_{c_i}{e(c_i)} \]
\(E\) counts the bonds in a configuration. Bonds are given negative value because they reduce the energy of the system.
Let \(S_n=\left\{C_i\right\}\) be a set of configurations of the first \(n\) beads in \(\mathcal{O}\)'s transcript \(b\). Let \(C^{\leftarrow k}\) be the configuration obtained by removing the last \(k\) beads in \(C\). Let \(C^{\rightarrow k}\) be the set of configurations obtainable by adding the next \(k\) beads in the transcript to \(C\). \(S^{\leftarrow k}=\{C^{\leftarrow k} | C \in S\}\) and \(S^{\rightarrow k}=\{X | X \in C^{\rightarrow k} \in S\}\).
An update \(H(S_n)\) on \(S_n\) is given by:
\[ H(S_n)=\begin{cases} \texttt{argmin }H\left(()^{\rightarrow n+1}\right) & n < \delta-1 \\ \bigcup_{\gamma \in S^{\leftarrow \delta-1}}{\texttt{argmin }H\left(\gamma^{\rightarrow \delta}\right)} & n \geq \delta-1 \end{cases} \]
In other words, updating a set of configurations of a subsequence of the transcript replaces each configuration with the set of configurations with one more bead from the transcript and minimum energy in the last \(\delta\) beads.
The set of possible end states of \(\mathcal{O}\) is given by \(H^n(\left\{()\right\})\), where \(n\) is the length of the transcript and \(()\) is an empty configuration.
Further consideration of the model is given by Geary, Meunier, Schabanel and Seki[1].
Turing-Completeness
Given the history-dependent nature of the RNA strand's energy level, it is reasonalbe to guess that the oritatami model permits Turing-complete computation. Indeed, this has been confirmed by Geary, Meunier, Schabanel and Seki, whose paper[2] showed that the oritatami model permits Turing-complete computation subject to only polynomial inflation in input size. This was shown as follows:
\[ \texttt{Oritatami} \rightarrow \texttt{Skipping Cyclic Tag Systems} \rightarrow \texttt{Cyclic Tag Systems} \rightarrow \texttt{Turing Machines} \]
Shape-Folding
Demaine et. al.[3] have shown the following. There are shapes which unfoldable by all OSs. It is NP-hard to answer the general question "Is this shape foldable by an OS?" However, it has been shown that every shape inflated 3 times is foldable by an OS with delay 1. Moreover, every shape inflated 2 times is foldable by an OS with some finite delay delta. In general, for any OS with delay \(\delta>2\), there are shapes which it can fold but which it cannot fold for any smaller delay \(\delta' < \delta\).
References
- ↑
Geary, Cody, Meunier, Pierre-Étienne, Schabanel, Nicolas, Seki, Shinnosuke - Oritatami: A Computational Model for Molecular Co-Transcriptional Folding
- International Journal of Molecular Sciences 20(9):2259, May 2019
- http://dx.doi.org/10.3390/ijms20092259
BibtexAuthor : Geary, Cody, Meunier, Pierre-Étienne, Schabanel, Nicolas, Seki, Shinnosuke
Title : Oritatami: A Computational Model for Molecular Co-Transcriptional Folding
In : International Journal of Molecular Sciences -
Address :
Date : May 2019
- ↑
Cody Geary, Pierre-Étienne Meunier, Nicolas Schabanel, Shinnosuke Seki - Proving the Turing Universality of Oritatami Co-Transcriptional Folding (Full Text)
- ↑
Erik D. Demaine, Jacob Hendricks, Meagan Olsen, Matthew J. Patitz, Trent A. Rogers, Nicolas Schabanel, Shinnosuke Seki, Hadley Thomas - Know When to Fold 'Em: Self-Assembly of Shapes by Folding in Oritatami