Difference between revisions of "Abstract Tile Assembly Model (aTAM)"
| Line 8: | Line 8: | ||
Given a set $T$ of tile types, an [[Assembly]] is a partial function ${\alpha}:{\mathbb{Z}^2} \dashrightarrow {T}$. An assembly is [[Assembly#Tau-stable Assembly| $\tau$-stable]] if it cannot be broken up into smaller assemblies without breaking bonds of total strength at least $\tau$, for some $\tau \in \mathbb{N}$. | Given a set $T$ of tile types, an [[Assembly]] is a partial function ${\alpha}:{\mathbb{Z}^2} \dashrightarrow {T}$. An assembly is [[Assembly#Tau-stable Assembly| $\tau$-stable]] if it cannot be broken up into smaller assemblies without breaking bonds of total strength at least $\tau$, for some $\tau \in \mathbb{N}$. | ||
| − | Self-assembly begins with a | + | Self-assembly begins with a [[Assembly#Seed Assembly| seed assembly]] $\sigma$ and |
proceeds asynchronously and nondeterministically, with tiles | proceeds asynchronously and nondeterministically, with tiles | ||
adsorbing one at a time to the existing assembly in any manner that | adsorbing one at a time to the existing assembly in any manner that | ||
| − | preserves $\tau$-stability at all times. A | + | preserves $\tau$-stability at all times. A [[Tile Assembly System (TAS)#Abstract Tile Assembly Model Tile Assembly System (aTAM TAS) | tile assembly system (TAS)]] is an ordered triple $\mathcal{T} = (T, \sigma, \tau)$, |
| − | ( | ||
where $T$ is a finite set of tile types, $\sigma$ is a seed assembly | where $T$ is a finite set of tile types, $\sigma$ is a seed assembly | ||
| − | with finite domain, and $\tau \in \N$. A | + | with finite domain, and $\tau \in \mathbb{N}$. A [[Tile Assembly System (TAS)#Abstract Tile Assembly Model Generalized Tile Assembly System (aTAM GTAS) | generalized tile assembly system (GTAS)]] |
| − | assembly system | ||
is defined similarly, but without the finiteness requirements. We | is defined similarly, but without the finiteness requirements. We | ||
| − | write $\ | + | write $\mathcal{A}[\mathcal{T}]$ for the set of all assemblies that can arise |
(in finitely many steps or in the limit) from $\mathcal{T}$. An | (in finitely many steps or in the limit) from $\mathcal{T}$. An | ||
| − | assembly $\alpha \in \ | + | assembly $\alpha \in \mathcal{A}[\mathcal{T}]}$ is [[Assembly#Terminal Assembly| terminal]], and we write $\alpha \in |
| − | \ | + | \mathcal{A}_{\Box}[\mathcal{T}]}$, if no tile can be $\tau$-stably added to it. It is clear that $\mathcal{A}_{\Box}[\mathcal{T}] \subset \mathcal{A}[\mathcal{T}]}$. |
An assembly sequence in a TAS $\mathcal{T}$ is a (finite or infinite) sequence $\vec{\alpha} = (\alpha_0,\alpha_1,\ldots)$ of assemblies in which each $\alpha_{i+1}$ is obtained from $\alpha_i$ by the addition of a single tile. The $\emph{result}$ $\res{\vec{\alpha}}$ of such an assembly sequence is its unique limiting assembly. (This is the last assembly in the sequence if the sequence is finite.) The set $\prodasm{T}$ is partially ordered by the relation $\longrightarrow$ defined by | An assembly sequence in a TAS $\mathcal{T}$ is a (finite or infinite) sequence $\vec{\alpha} = (\alpha_0,\alpha_1,\ldots)$ of assemblies in which each $\alpha_{i+1}$ is obtained from $\alpha_i$ by the addition of a single tile. The $\emph{result}$ $\res{\vec{\alpha}}$ of such an assembly sequence is its unique limiting assembly. (This is the last assembly in the sequence if the sequence is finite.) The set $\prodasm{T}$ is partially ordered by the relation $\longrightarrow$ defined by | ||
Revision as of 17:09, 21 May 2013
Informal Description of the Model
The aTAM was developed to, in some sense, be an effectivization of Wang tiling. (See Wang Tiling for more about this relationship.) Namely, it provides a defined process by which an initial (called the seed) assembly can grow into a resultant structure. This is essentially accomplished by assigning a positive integer strength value to each edge color in a set of Wang tiles and stipulating that when two tile edges are adjacent, if their colors match then the edges bind with force equivalent to the strength of the edge color. Then, starting with a preformed seed assembly (usually taken to be a single tile of a specified type), additional tiles can attach one at a time as long as the sum of the strengths of the bonds that each makes with tiles already in the assembly meets a system wide threshold value called the Temperature.
Formal Definition of the Model
We now give a brief formal definition of the aTAM. See [1] [2] [3] [4] for other developments of the model. Our notation is that of [4], which also contains a more complete definition.
Given a set \(T\) of tile types, an Assembly is a partial function \({\alpha}:{\mathbb{Z}^2} \dashrightarrow {T}\). An assembly is \(\tau\)-stable if it cannot be broken up into smaller assemblies without breaking bonds of total strength at least \(\tau\), for some \(\tau \in \mathbb{N}\).
Self-assembly begins with a seed assembly \(\sigma\) and proceeds asynchronously and nondeterministically, with tiles adsorbing one at a time to the existing assembly in any manner that preserves \(\tau\)-stability at all times. A tile assembly system (TAS) is an ordered triple \(\mathcal{T} = (T, \sigma, \tau)\), where \(T\) is a finite set of tile types, \(\sigma\) is a seed assembly with finite domain, and \(\tau \in \mathbb{N}\). A generalized tile assembly system (GTAS) is defined similarly, but without the finiteness requirements. We write \(\mathcal{A}[\mathcal{T}]\) for the set of all assemblies that can arise (in finitely many steps or in the limit) from \(\mathcal{T}\). An assembly \(\alpha \in \mathcal{A}[\mathcal{T}]}\) is terminal, and we write \(\alpha \in \mathcal{A}_{\Box}[\mathcal{T}]}\), if no tile can be \(\tau\)-stably added to it. It is clear that \(\mathcal{A}_{\Box}[\mathcal{T}] \subset \mathcal{A}[\mathcal{T}]}\).
An assembly sequence in a TAS \(\mathcal{T}\) is a (finite or infinite) sequence \(\vec{\alpha} = (\alpha_0,\alpha_1,\ldots)\) of assemblies in which each \(\alpha_{i+1}\) is obtained from \(\alpha_i\) by the addition of a single tile. The \(\emph{result}\) \(\res{\vec{\alpha}}\) of such an assembly sequence is its unique limiting assembly. (This is the last assembly in the sequence if the sequence is finite.) The set \(\prodasm{T}\) is partially ordered by the relation \(\longrightarrow\) defined by
\(\begin{eqnarray*} \alpha \longrightarrow \alpha' & \textmd{iff} & \textmd{there is an assembly sequence } \vec{\alpha} = (\alpha_0,\alpha_1,\ldots) \\& & \textmd{such that } \alpha_0 = \alpha \textmd{ and } \alpha' = \res{\vec{\alpha}}\\. \end{eqnarray*}\)
We say that \(\mathcal{T}\) is \(\emph{directed}\) (a.k.a. \(\emph{deterministic}\), \(\emph{confluent}\), \(\emph{produces a unique assembly}\)) if the relation \(\longrightarrow\) is directed, i.e., if for all \(\alpha,\alpha' \in \prodasm{T}\), there exists \(\alpha'' \in \prodasm{T}\) such that \(\alpha \longrightarrow \alpha''\) and \(\alpha' \longrightarrow \alpha''\). It is easy to show that \(\mathcal{T}\) is directed if and only if there is a unique terminal assembly \(\alpha \in \prodasm{T}\) such that \(\sigma \longrightarrow \alpha\).
In general, even a directed TAS may have a very large (perhaps uncountably infinite) number of different assembly sequences leading to its terminal assembly. This seems to make it very difficult to prove that a TAS is directed. Fortunately, Soloveichik and Winfree [5] have defined a property, {\it local determinism}, of assembly sequences and proven the remarkable fact that, if a TAS \(\mathcal{T}\) has {\it any} assembly sequence that is locally deterministic, then \(\mathcal{T}\) is directed. Intuitively, an assembly sequence \(\vec{\alpha}\) is locally deterministic if (1) each tile added in \(\vec{\alpha}\) ``just barely binds to the existing assembly (meaning that is does so with a summed strength of bonds equal to exactly \(\tau\)); (2) if a tile of type \(t_0\) at a location \(\vec{m}\) and its immediate ``output-neighbors (i.e. those adjacent tiles which bound after the tile at \(\vec{m}\)) are deleted from the \({\it result}\) of \(\vec{\alpha}\), then no tile of type \(t \ne t_0\) can attach itself to the thus-obtained configuration at location \(\vec{m}\); and (3) the result of \(\vec{\alpha}\) is terminal.
A set \(X \in \mathbb{Z}^2\) \({\it weakly self-assembles}\) if there exists
a TAS \({\mathcal T} = (T, \sigma, \tau)\) and a set \(B \subseteq T\)
such that \(\alpha^{-1}(B) = X\) holds for every terminal assembly
\(\alpha \in \termasm{T}\). Essentially, weak self-assembly can be thought of
as the creation (or ``painting) of a pattern of tiles from \(B\) (usually taken to be a
unique ``color) on a possibly larger ``canvas of un-colored tiles.
A set \(X\) \(\emph{strictly self-assembles}\) if there is a TAS \(\mathcal{T}\) for which every assembly \(\alpha\in\termasm{T}\) satisfies \(\dom \alpha = X\). Essentially, strict self-assembly means that tiles are only placed in positions defined by the shape. Note that if \(X\) strictly self-assembles, then \(X\) weakly self-assembles. (Let all tiles be in \(B\).)
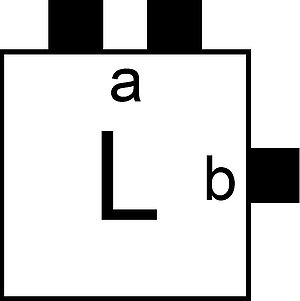
Tiles are often depicted as squares whose various sides contain 0, 1, or 2 attached black squares,
indicating whether the glue strengths on
these sides are 0, 1, or 2, respectively. Thus, for example, a tile
of the type shown to the right has glue of strength 0 on the left (W) and bottom (S), glue of color `a' and
strength 2 on the top (N), and glue of color `b' and strength 1 on the
right (E). This tile also has a label `L', which plays no formal role
but may aid our understanding and discussion of the construction.
References
- ↑
Erik Winfree - Algorithmic Self-Assembly of DNA
- Ph.D. Thesis, California Institute of Technology , June 1998
- BibtexAuthor : Erik Winfree
Title : Algorithmic Self-Assembly of DNA
In : Ph.D. Thesis, California Institute of Technology -
Address :
Date : June 1998
- ↑
Paul W. K. Rothemund, Erik Winfree - The Program-size Complexity of Self-Assembled Squares (extended abstract)
- STOC '00: Proceedings of the thirty-second annual ACM Symposium on Theory of Computing pp. 459--468, Portland, Oregon, United States,2000
- BibtexAuthor : Paul W. K. Rothemund, Erik Winfree
Title : The Program-size Complexity of Self-Assembled Squares (extended abstract)
In : STOC '00: Proceedings of the thirty-second annual ACM Symposium on Theory of Computing -
Address : Portland, Oregon, United States
Date : 2000
- ↑
Paul W. K. Rothemund - Theory and Experiments in Algorithmic Self-Assembly
- Ph.D. Thesis, University of Southern California , December 2001
- BibtexAuthor : Paul W. K. Rothemund
Title : Theory and Experiments in Algorithmic Self-Assembly
In : Ph.D. Thesis, University of Southern California -
Address :
Date : December 2001
- ↑ 4.0 4.1
James I. Lathrop, Jack H. Lutz, Scott M. Summers - Strict Self-Assembly of Discrete Sierpinski Triangles
- Theoretical Computer Science 410:384--405,2009
- BibtexAuthor : James I. Lathrop, Jack H. Lutz, Scott M. Summers
Title : Strict Self-Assembly of Discrete Sierpinski Triangles
In : Theoretical Computer Science -
Address :
Date : 2009
- ↑
David Soloveichik, Erik Winfree - Complexity of Self-Assembled Shapes
- SIAM Journal on Computing 36(6):1544-1569,2007
- BibtexAuthor : David Soloveichik, Erik Winfree
Title : Complexity of Self-Assembled Shapes
In : SIAM Journal on Computing -
Address :
Date : 2007