Signal-passing Tile Assembly Model (STAM)

The signal tile assembly model(STAM) describes a signaled tile self assembly process that enriches the tile assembly paradigm with improved capabilities and allows tile assembly to more closely emulate biological and natural processes.

Signaled glue activation was introduced for the purpose of allowing supertiles to take on new identities or roles once assembled [2], so that supertile interactions as described in hierarchical models such as the 2HAM can simulate the interactions of individual tiles.

The generalized model presented here has been designed to take into consideration a DNA implementation of all aspects of signaled assembly: binding, signaling, and glue activation or deactivation.

The addition of signaled glue activation and deactivation to tile assembly brings it one step closer to emulating biological processes of self assembly, where communication within a developing and growing living organism are crucial to its survival and success. Communication between tiles and throughout assemblies allows them to take on changing roles in hierarchical assembly processes, resulting in production of organized entities that could continue to function as elements in further tile computation.

Physical Basis for the Model

The physical body of a tile might be composed entirely from a DNA origami structure which has more room for signal pathways than smaller DNA structures that have been used to implement the passive tiles of the TAM. Toe-hold mediated DNA strand exchange mechanisms [3-6], as shown in Figure 1, provide a basis for a plausible physical implementation of signaling, glue activation and glue deactivation. Signals across individual tiles could potentially be implemented using DNA hybridization cascades such as HCR [7], transducers [8], seesaw gates [9], other mechanisms [10], or by DNA walkers [11-14].

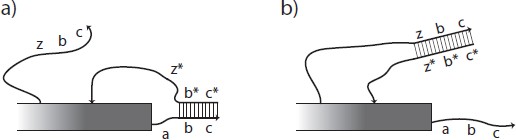
Fig. 1: Activation of a latent glue. Single-stranded DNA is depicted as a line with an arrow at the 3' end and double- stranded DNA is shown as two parallel lines connected by a ladder of base pairs. Letters such as a and y indicate short sequences of DNA bases and a star indicates the complementary sequence. Rectangles indicate structures, possibly composed of DNA origami, to which the relevant sticky ends of DNA are attached. a) The strand zbc is presumed to be unavailable until freed by a previous signaling cascade (not shown). The sequence labeled z may then bind at the toehold z8 on the protection strand c* b* z*, removing it from the glue strand abc via strand displacement. The protection strand is shown bound only to b and c, which is enough to prevent interaction with the complementary tile edge shown as long as no toeholds are free to interact. Alternatively, the entire sequence abc could be blocked by the protection strand. b) Once the protection strand is removed, the glue strand abc is active or on.

A glue may be considered 'latent' or 'off' if its DNA sticky end is blocked by being bound to a complementary DNA strand. Activation of a latent glue can be done by the toe-hold mediated removal of a protection strand that blocks a sticky end, (Figure 1). Deactivation can be accomplished by a toehold-mediated mechanism that is essentially the reverse of activation, whereby a protection strand can be released in the vicinity of the glue strand, covering up the sticky end used for binding. By adding more toeholds, one could add a finite number of cycles of activation and deactivation, but each would be mediated by a different activation and deactivation strand, and each effectively consumes DNA fuel. Thus, in the model we have limited activation to occurring only once. More instances of a glue can be added in a construction if needed.

STAM Notation and Model

High Level Description of the STAM

In the STAM, tiles are allowed to have sets of glues on each edge (as opposed to only one glue per side as in the TAM and 2HAM ). Tiles have an initial state in which each glue is either "on" or "latent" (i.e. can be switched on later). Tiles also each implement a transition function which is executed upon the binding of any glue on any edge of that tile. The transition function specifies a set of glues (along with the sides on which those glues are located) and an action for each: 1. turn that glue on (only valid if it is currently latent), or 2. turn that glue off (valid if it is currently on or latent). Note that turning a glue off breaks any bond that that glue may have formed with a neighboring tile. The transition function defined for each tile type is allowed a unique set of output actions for the binding event of each glue along its edges. As the STAM is an extension of the 2HAM, binding and breaking can occur between pairs of arbitrarily sized supertiles. In order to allow for physical mechanisms which implement the transition functions of tiles but are arbitrarily slower or faster than the average rates of (super)tile attachments and detachments, rather than immediately enacting the outputs of transition functions, each output action is put into a set of "pending actions" which includes all actions which have not yet been enacted for that glue. An STAM system consists of a set of tiles and a temperature value. To define what is producible from such a system, we use a recursive definition of producible assemblies which starts with the initial tiles and then contains any supertiles which can be formed by doing the following to any producible assembly: 1. executing any entry from the pending actions of any one glue within a tile within that supertile (and then that action is removed from the pending set), 2. binding with another supertile if they are able for form a \(\tau\)-stable supertile, or 3. breaking apart into 2 separate supertiles along a cut whose total strength is less than \(\tau\).

Basic Notation

Let \(D\) denote the set of labels \(\{north, south, east, west\}\), or \(\{N,S,E,W\}\).

Active Glues and Glue States

Let \(\Gamma\) denote a set of \(glue types\). A \(glue\) is an ordered pair \((g,s)\) where \(g \in \Gamma\) is the glue type and \(s \in \mathbb{Z}\) is the glue \(strength\). Note that throughout the remainder of this paper, unless specifically stated, all glues will have strength \(1\) and as shorthand will be denoted simply by their glue types with the strength omitted.

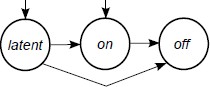
Let \(Q = \{\texttt{latent}, \texttt{on}, \texttt{off}\}\) be the set of possible \(states\) for a glue. Intuitively, \(\texttt{on}\) is the ``normal, active state of a glue, meaning that it is either able to bind or currently bound. A glue in the \(\texttt{latent}\) state is inactive (and therefore unable to bind), and also has never been \(\texttt{on}\) (or \(\texttt{off}\)). A glue in the \(\texttt{off}\) state is also inactive and unable to bind, but can never be (re)activated. We define an \(active glue\) as an ordered pair \((g,q)\) where \(g \in \Gamma\) is a glue type and \(q \in Q\) is a state.

Fig. 2: The valid state transitions for active glues

Active Labels

As in the original TAM, we define a \(label\) as an arbitrary string over some fixed alphabet and labels will be used as non-functional (i.e. they don't participate in tile bindings) means of identifying tile types. Denote as \(\Sigma\) the set of all valid labels. For the self-assembly of patterns (e.g. the weak self-assembly of the Sierpinski triangle), tile labels are the mechanism used for distinguishing between groups of tiles, i.e. those ``in the pattern and those ``outside it. Experimentally, labels can be implemented as DNA loops which protrude above the surfaces of tiles for imaging purposes [12], and thus the motivation exists to allow for the modification of tile labels along with glues. Therefore, we define an \(active label\) is an ordered pair \((x,q)\) where \(x \in \Sigma\) and \(q \in Q\).

Active Tiles and Transition Functions

A \(generalized active tile type\) \(t\) is a unit square defined as a \(4\)-tuple \(t = \left(G, L, \delta, \Pi\right)\) where \(G: D \rightarrow P(\Gamma \times Q)\) is a function specifying the set of all active glues present on a given side, \(L\) is the set of all active labels, \(\delta: D \times \Gamma \rightarrow P(((D \times \Gamma \times \{\texttt{on}, \texttt{off}\}) \cup (\Sigma \times \{\texttt{on}, \texttt{off}\}))\) is the \(transition function\) and \(\Pi\) is a multiset over \((D \times \Gamma \times \{\texttt{on}, \texttt{off}\}) \cup (\Sigma \times \{\texttt{on}, \texttt{off}\})\). A generalized active tile type \(t = (G, L, \delta, \Pi)\) is an \(active tile type\) if, for all \(d \in D\) and for all active glues \((g,q),(g',q') \in G(d)\), \(g \ne g'\). In other words, while a tile side may have multiple glues, there cannot be multiple copies of the same type of glue on a single side.

A transition function \(\delta\) takes as input a direction \(d \in D\) and a glue type \(g \in \Gamma\) (i.e. we say that it is ``fired by the binding of glue type \(g\) on side \(d\) of \(t\)), and outputs a (possibly empty) set of \(glue\) or \(label actions\), i.e., elements of \((D \times \Gamma \times \{\texttt{on}, \texttt{off}\}) \cup (\Sigma \times \{\texttt{on}, \texttt{off}\})\). Consider an active tile type \(t = (G, L, \delta, \Pi)\) and suppose that \((g,q) \in G(d)\) for some \(d \in D\) and \((d', g' ,q') \in \delta(d,g)\). Intuitively, if \(m = \Pi(d', q')\) (i.e., the \(multiplicity\) of \((d',q') \in \Pi\)) \(before\) \(\delta\) ``fires, then \(\Pi(d', q') = m + 1\) \(after\) executing \(\delta\). We assume for the sake of convenience that \(\delta\) outputs the empty set for any pair of direction and glue on which \(\delta\) is not explicitly defined. In other words, the binding of a glue on \(t\) fires the transition function, which can result in a set of ``requests for specific active glues and labels on \(t\) to transition into specified states.

Active Supertiles

Active supertiles in the STAM are defined similarly to supetiles in the 2HAM. Note that only glues which are in the \(\texttt{on}\) state can bind, and only those which are bound contribute to the \(\tau\)-stability of a supertile. When two \(\tau\)-stable supertiles can be translated so that they are non-overlapping and the abutting \(\texttt{on}\) glues can bind to create a cut strength of at least \(\tau\), we say that they are \(\tau\)-\(combinable\). A supertile \(A\) is said to be \(\tau\)-\(breakable\) into supertiles \(B\) and \(C\) if there exists a strength \(\tau' < \tau\) strength cut of the stability graph \(G_A\) that separates the tiles of \(A\) into supertiles \(B\) and \(C\).

Active Supertile Combination

Two active supertiles \(A\) and \(B\) may combine into active supertile \(C\) if the underlying supertiles for \(A\) and \(B\) are \(\tau\)-combinable into the underlying supertile for \(C\). When supertiles combine, all matched glues in the \(\texttt{on}\) state on the boundary between \(A\) and \(B\) are said to bind, and thus fire the transition functions of their respective tiles, causing the necessary states to be added to the pending sets of the targeted tiles.

Active Supertile Breaking

An active supertile \(A\) can break into active supertiles \(B\) and \(C\) if the underlying supertile for \(A\) has a cut of less than \(\tau\)-strength dividing \(A\) into the underlying supertiles for \(B\) and \(C\).

References

1. Jennifer E. Padilla, Matthew J. Patitz, Raul Pena, Robert T. Schwellery, Nadrian C. Seeman, Robert Sheline, Scott M. Summers, and Xingsi Zhong, Asynchronous Signal Passing for Tile Self-Assembly: Fuel Efficient Computation and Efficient Assembly of Shapes

2. J.E. Padilla, W. Liu, and N.C. Seeman, Hierarchical self assembly of patterns from the Robinson tilings: DNA tile design in an enhanced tile assembly model, Natural Computing online first, 17 August 2011 (2011).

3. G. Seelig, D. Soloveichik, D.Y. Zhang, and E. Winfree, Enzyme-free nucleic acid logic circuits, science 314 (2006), no. 5805, 1585.

4. P. Yin, H.M.T. Choi, C.R. Calvert, and N.A. Pierce, Programming biomolecular self-assembly path- ways, Nature 451 (2008), no. 7176, 318-322.

5. B. Yurke, A.J. Turberfield, A.P. Mills, F.C. Simmel, and J.L. Neumann, A DNA-fuelled molecular machine made of DNA, Nature 406 (2000), no. 6796, 605-608.

6. D.Y. Zhang and G. Seelig, Dynamic DNA nanotechnology using strand-displacement reactions, Nature Chemistry 3 (2011), no. 2, 103-113.

7. R.M. Dirks and N.A. Pierce, Triggered amplification by hybridization chain reaction, Proceedings of the National Academy of Sciences of the United States of America 101 (2004), no. 43, 15275.

8. G. Seelig, D. Soloveichik, D.Y. Zhang, and E. Winfree, Enzyme-free nucleic acid logic circuits, science 314 (2006), no. 5805, 1585.

9. L. Qian and E. Winfree, A simple DNA gate motif for synthesizing large-scale circuits, DNA Com- puting (2009), 70-89.

10. P. Yin, H.M.T. Choi, C.R. Calvert, and N.A. Pierce, Programming biomolecular self-assembly path- ways, Nature 451 (2008), no. 7176, 318-322.

11. K. Lund, A.J. Manzo, N. Dabby, N. Michelotti, A. Johnson-Buck, J. Nangreave, S. Taylor, R. Pei, M.N. Stojanovic, and N.G. Walter, Molecular robots guided by prescriptive landscapes, Nature 465 (2010), no. 7295, 206{210.

12. T. Omabegho, R. Sha, and N.C. Seeman, A bipedal DNA brownian motor with coordinated legs, Science 324 (2009), no. 5923, 67.

13. S.F.J. Wickham, M. Endo, Y. Katsuda, K. Hidaka, J. Bath, H. Sugiyama, and A.J. Turberfield, Di- rect observation of stepwise movement of a synthetic molecular transporter, Nature Nanotechnology 6 (2011), no. 3, 166-169.

14. P. Yin, H.M.T. Choi, C.R. Calvert, and N.A. Pierce, Programming biomolecular self-assembly path- ways, Nature 451 (2008), no. 7176, 318-322.