Maze-Walking Tile Assembly Model
Overview
A typical aTAM tile set capable of universal computation can be quite large. Using mazes consisting of polyominoes, much smaller tile sets can be capable of universal computation as well[1]. By using the walls of mazes as a guiding force, Cook et al. (2021) show how to simulate any arbitrary Boolean circuit with their Maze-Walking Tile Assembly Model (TAM).
Construction
The maze itself is constructed from polyomino tiles, where exposed edges can have a glue to attach to the standard square tiles. The inputs to the maze's entrances are standard tiles (like those of the aTAM) representing zeros or ones. The authors provide a tiny (4-tile) tile set capable of computing the output of a Boolean circuit by solving the maze, which is constructed according to the circuit[1] (more on that later).
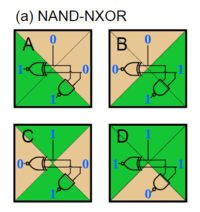
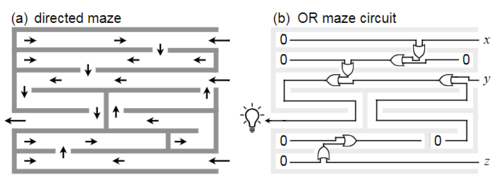
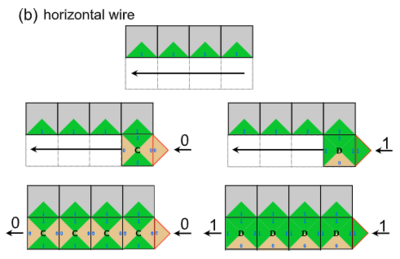
In the above figure of the authors' NAND-NXOR tile set, you can think of the northern and eastern edges of the tiles as bit inputs, the western edge as the result of an NXOR operation on those inputs, and the southern edge as a NAND operation on the inputs. Now, in order to utilize these tiles, a given circuit must be converted to its corresponding maze. When representing a simple circuit wire, the walls of the maze are lined with "1" glues. These facilitate the growth of the tiles that represent signals throughout the maze, and an example from the authors can be seen below.
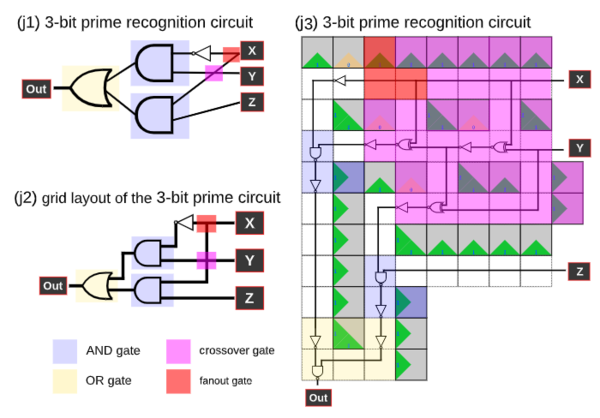
The authors give individual constructions of various turns, fanouts, logic gates, and crossover gates (used to convert crossing wires to something that works in only two dimensions) in the paper. Below, you can find an example circuit that employs many of these constructions to detect 3-bit prime numbers. The interested reader can find a terminal assembly given an input as an example in Figure 3 of [1].