Equivalence of Cellular Automata and the Tile Assembly Model

Abstract

We explore relationships between two models of systems which are governed by only the local interactions of large collections of simple components: cellular automata (CA) and the abstract Tile Assembly Model (aTAM). While sharing several similarities, the models have fundamental differences, most notably the dynamic nature of CA (in which every cell location is allowed to change state an infinite number of times) versus the static nature of the aTAM (in which tiles are static components that can never change or be removed once they attach to a growing assembly). We work with 2-dimensional systems in both models, and for our results we first define what it means for CA systems to simulate aTAM systems, and then for aTAM systems to simulate CA systems. We use notions of simulate which are similar to those used in the study of intrinsic universality since they are in some sense strict, but also intuitively natural notions of simulation. We then demonstrate a particular nondeterministic CA which can be configured so that it can simulate any arbitrary aTAM system, and finally an aTAM tile set which can be configured so that it can be used to simulate any arbitrary nondeterministic CA system which begins with a finite initial configuration.

Definitions

Intrinsic universality is a notion where one model is capable of simulating the behavior of any model within a class of model in such a way that a scaling of the simulator with respect to size and time can be mapped to a configuration of the simulated model. This differs from computational simulation and the notion of Turing universality where the components of the model can simulate the components of another model but not the behavior of the components.

Cellular automata (CA) consists of an infinite grid of cells which can each sense their immediate neighborhoods and then all independently but synchronously update their states based on finite set of rules and the state of their neighborhoods. The abstract Tile Assembly Model (aTAM) consists of individual square “tile” components that have “glues” on their edges that allow the tiles to autonomously bind together to form structures based only on the amount and strengths of the matching glues on edges of adjacent tiles.

Overview

It has been shown that the aTAM is intrinsically universal by creating a tile set \(\mathcal{U}\) that for any aTAM tile assembly system \(\mathcal{T}\) of any temperature, \(\mathcal{U}\) can create a seed structure dependent on \(\mathcal{T}\) so the resulting system at temperature 2 simulates the behavior of \(\mathcal{T}\) . The aTAM has also been called an asynchronous, nondeterministic CA where quiescent states that change to “tile” states never change again. In addition, showed 2D aTAM can simulate 1D CA and showed 3D aTAM can simulate 2D. This led to exploration of simulations between two models using the same dimension for each, specifically 2D, with the challenge of overcoming the fundamental differences between the static nature of aTAM and the dynamic nature of CA

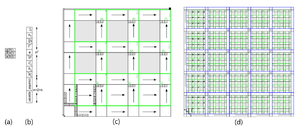
The authors show that 2D aTAM can simulate 2D CA by using a scalable representation function and an \textit{n} \(\times\) \textit{n} square that grow 1 cell row on each side of the square at every step. This recursive, “in-place” simulation maps an infinite hierarchy of every subassembly within it at smaller scale factors to unique cells at some time step. They also show that that 2D CA can simulate 2D aTAM using a single token to traverse a configuration of a neighborhood with quiescent states, token states, tile states, and bridge tiles states. Single state changes from a quiescent state to a tile state corresponds to adding single tiles in the aTAM system.

Results

Figure 1 is an initial configuration obtained from an initial assembly before (a) and after (b) changing states along paths connecting disjoint regions of quiescent cells to bridge tile states. Grey cells denote cells in any tile state while cells labeled B denote cells in bridge tile states. The cell labeled T is in token state left.

There is a single nondeterministic, synchronous CA \(\mathcal{A}\) that for any aTAM system \(\mathcal{T}\) can be given an initial configuration dependent on \(\mathcal{T}\) so it will exactly simulate \(\mathcal{T}\). The initial configuration of \(\mathcal{A}\) is created by mapping each seed tile in \(\mathcal{T}\) to the corresponding tile state in \(\mathcal{A}\), adding corresponding bridge tiles states to connect disjoint regions of connected quiescent cells, and adding a cell in token state left tile above a cell in a tile state.

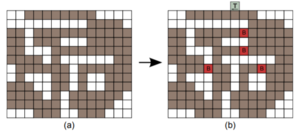
There is also a single aTAM tile set \(\mathcal{S}\) that, for any nondeterministic, synchronous CA \(\mathcal{C}\) which begins with all the cells in a quiescent state except for a finite number of cells forming the initial configuration, can be given an initial seed configuration for \(\mathcal{S}\) dependent upon \(\mathcal{C}\) so it will exactly simulate \(\mathcal{C}\). The initial seed configuration for \(\mathcal{S}\) is a single column of cells (Figure 2b) that starts from the bottom and goes up as it encodes the \(mathit{n}\) \(\times\) \(\mathit{n}\) block of cells in the initial configuration of \(\mathcal{C}\) (Figure2a) starting from the bottom and going left to right then up.

Both of these results were in 2-dimensional discrete space.

Figure 2 depicts the initial configuration of a CA system (a), the initial configuration of an aTAM simulating the CA system (b), and the aTAm formation representing the CA system at time step 0 (c) and 1(d)