Strict Self-Assembly of Fractals using Multiple Hands

This paper demonstrates the capability of the h-HAM model, itself a generalization of the 2HAM model, to strictly self-assemble a subset of fractal shapes.

Abstract

In this paper we consider the problem of the strict self-assembly of infinite fractals within tile self-assembly. In particular, we provide tile assembly algorithms for the assembly of the discrete Sierpinski triangle and the discrete Sierpinski carpet within a class of models we term the h-handed assembly model(h-HAM), which generalizes the 2-HAM to allow up to h assemblies to combine in a single assembly step.Despite substantial consideration, no purely growth self-assembly model has yet been shown to strictly assemble an infinite fractal without significant modification to the fractal shape. In this paper we not only achieve this, but in the case of the Sierpinski carpet are able to achieve it within the 2-HAM, one of the most well studied tile assembly models in the literature. Our specific results are as follows. We provide a 6-HAM construction for the Sierpinski triangle that works at scale factor 1, 30 tile types, and assembles the fractal in a near perfect way in which all intermediate assemblies are finite-sized iterations of the recursive fractal. We further assemble the Sierpinski triangle within the 3-HAM at scale factor 3and 990 tile types. For the Sierpinski carpet, we present a 2-HAM result that works at scale factor 3and uses 1,216 tile types. We further include analysis showing that the aTAM is incapable of strictly assembling the non-tree Sierpinski triangle considered in this paper, and that multiple hands are needed for the near-perfect assembly of the Sierpinski triangle and the Sierpinski carpet.

Overview

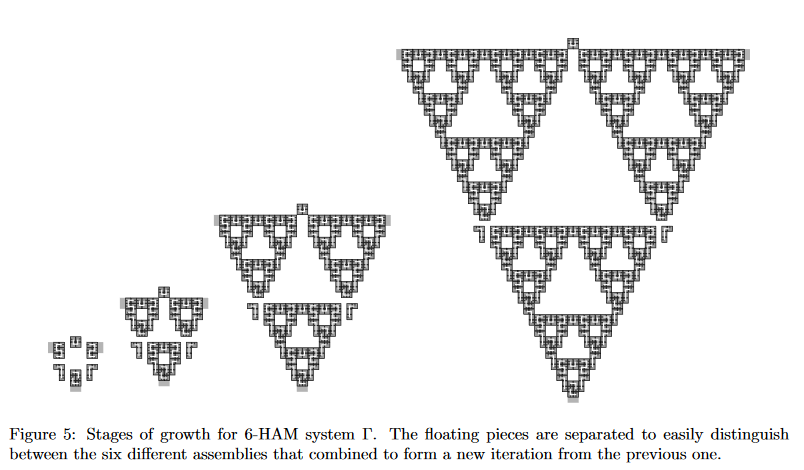
This paper introduces an generalization of the 2HAM model called h-HAM, the primary difference of which is the possibility for up to h different sub assemblies to combine at a given step. Hence, the above figure refers to 3-HAM, wherein up to three assemblies may combine at a single time, and 6-HAM, wherein up to six different assemblies may combine. The authors focus their efforts on the assembly of an instance of the (non-tree version of the) self similar discrete Sierpinski triangle and the Sierpinski carpet. Notably, the authors demonstrate a construction of the Sierpinski triangle which assembles at a scale factor of one, demonstrating the power added to the 2HAM model with the addition of more assemblies to a given combination step. The authors introduce a term they dub near perfect assembly, in which the intermediate assemblies of the system are almost exactly the finite-sized iterations that define the infinite fractal shape.

Impossibility Results

The authors prove that the discrete Sierpinski triangle does not strictly self assemble in any aTAM system, based on an intuitive window movie principle argument that would force the assembly to produce periodic instead of self similar growth at the choke points that connect different iterations of the triangle. The authors further prove that in order for their near perfect assembly condition to be met, a hHAM system must use at least three or eight hands to nearly perfectly assemble the Sierpinski triangle and carpet, respectively.