Geometric Tile Assembly Model (GTAM)
Contents
Abstract
Nature is filled with examples of self-assembling systems. Some of the systems can be made from impressively small sets, such as proteins that assembly from 20 amino acids. Despite the size of the sets, these systems can still achieve a large variety of structures and functions by utilizing geometry. The particular 3-dimensional shape that a protein folds into is determined by the exact sequence of amino acids that compose it, and this shape determines the protein’s function. However, the geometries are often extremely complex and hard to predict. This use of geometry to encode information inspired the geometric tile assembly model (GTAM), which extends the aTAM by using tile types that have rigid geometries along each tile face. The GTAM allows increased efficiency for tile type complexity and simulation of computationally universal temperature 2 aTAM systems at temperature 1. The two-handed planar geometric tile assembly model (2GAM) which extends the GTAM and the 2HAM is also developed. [1].
Overview
The geometric tiles used in the GTAM have a glue and a geometric on each face. The geometric faces of two tiles are compatible if the tiles come together adjacently without any of their adjacent geometries overlapping.
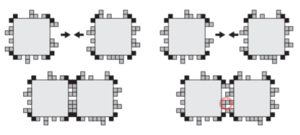
The position of the glues prevents bonding if there would be overlap because the incompatible geometries would not allow the glues to touch. This geometric hindrance ensures bonds cannot occur if the faces are not compatible. Tiles cannot rotate in GTAM in the same way as aTAM and also uses seeded tile assembly, but of course a tile type cannot attach to the supertile in an incompatible way. [1] [2]
The 2GAM extends the GTAM by allowing large separate assemblies to attach to each other as long as the sides are compatible. However, the two supertiles must not only be compatible with glues that are equal, have strength at least \(\tau\), and do not overlap, but must also be able to slide into place on the 2D plane without collision. The set of producible supertiles in the 2GAM consists of supertiles made of a single tile as well as any supertile that can be made using any two producible tiles that wouldn’t collide but would be \(\tau\)-stable. Terminally produced supertiles are a subset of producible tiles to which no other producible assembly can attach. [1]
Results
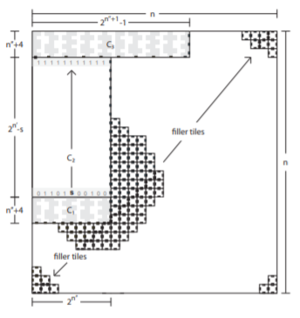
The authors demonstrate that \(\Theta\)(\(\sqrt{\log n}\)) distinct geometric tile types can assemble \(\mathit{n}\) \(\times\) \(\mathit{n}\) squares, which is an improvement from the \(\Theta\)(\(\log n /\log \log n\)) tile complexity required in the aTAM to assemble the same shape. The upper bound of \(O\)(\(\sqrt{\log n}\)) was constructed by creating a roughly 2 \(\times\) \(\log n\) rectangle to encode a \(\log n\) digit binary number and converting such a zig-zag system from temperature 2 to temperature 1. They also use two theorems to show that temperature 1 GTAM can simulate zig-zag, temperature 2 aTAM systems that are computationally universal without an increase in the number of unique tiles types required or the size of the assembly.
Additionally, the tile complexity to build a square in the 2HAM can be reduced to \(O\)(\(\log \log n\)) tile types if done in with geometric tiles in the 2GAM, the two-handed variant of the GTAM. However, 2GAM requires complex (\(O\)(\(\log n \log \log n\))) tile geometries with disconnect components and is constrained by 2-dimensional planarity. The authors also try to minimize the size of the necessary geometries by analyzing problems related to computing the necessary tile geometry patterns for the desired compatibilities between tiles. The solutions to the problems show the feasibility and limitations of designing geometric tile faces.