Non-cooperatively assembling large structures:a 2D pumping lemma cannot be as powerful as its 1D counterpart.

Abstract

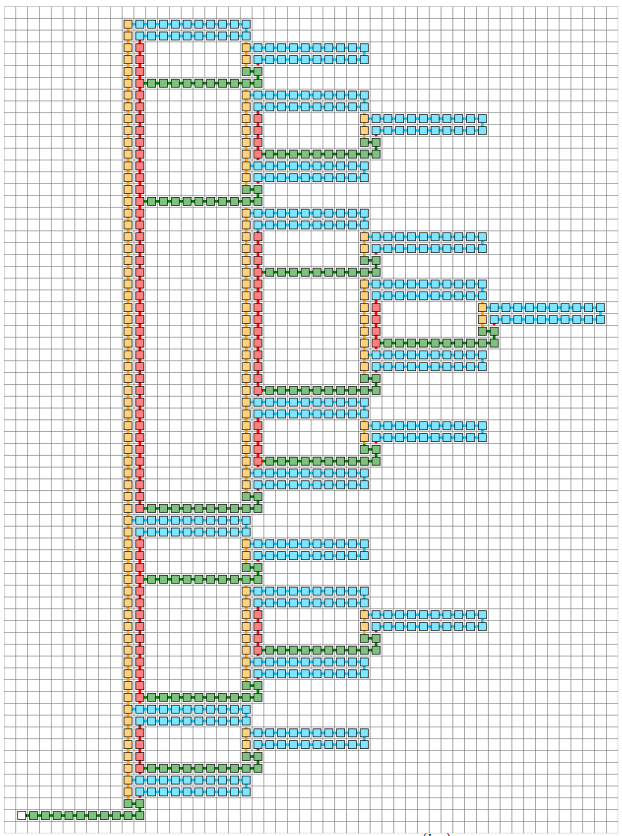
We show the first asymptotically efficient constructions in the so-called ”non cooperative planar tile assembly” model.Algorithmic self-assembly is the study of the local, distributed, asynchronous algorithms ran by molecules to self-organize, in particular during crystal growth. The general cooperative model, also called”temperature 2”, uses synchronization to simulate Turing machines, build shapes using the smallest possible amount of tile types, and other algorithmic tasks. However,in the non-cooperative (”temperature 1”) model, the growth process is entirely asynchronous,and mostly relies on geometry. Even though the model looks like a generalization of finite automata to two dimensions, its 3D generalization is capable of performing arbitrary (Turing)computation [SODA 2011], and of universal simulations [SODA 2014], whereby a single 3Dnon-cooperative tile set can simulate the dynamics of all possible 3D non-cooperative systems,up to a constant scaling factor.However, we showed in [STOC 2017] that the original 2D non-cooperative model is not capable of universal simulations, and the question of its computational power is still widely open. Here, we show an unexpected result, namely that this model can reliably grow assemblies of size Ω(n log(n)) with only n tile types, which is the first asymptotically efficient positive construction.

Overview

The authors present an argument and construction demonstrating the possibility of efficient non-cooperative assembly of an (n log(n)) width construction, using only n tile types. This serves to illustrate that there exists no linear pumping lemma for the 2D plane bound non-cooperative systems. Path and geometrical arguments serve as the primary motivators for the conclusion the authors drew. They further refer to an earlier work by the same authors, , which proved the existence of a non-linear pumping lemma for 2D non-cooperative assembly systems.

A terminal assembly demonstrating a greater than linear width construction given only n tile types. Different colors represent different predetermined paths.

References

}