4-sided Fractals in the 2HAM
Constructing a subset of fractals in the 2-handed assembly model.
Abstract
We consider the self-assembly of fractals in one of the most well-studied models of tile based self-assembling systems known as the Two-handed Tile Assembly Model (2HAM). In particular, we focus our attention on a class of fractals called discrete self-similar fractals (a class of fractals that includes the discrete Sierpinski carpet). We present a 2HAM system that finitely self-assembles the discrete Sierpinski carpet with scale factor 1. Moreover, the 2HAM system that we give lends itself to being generalized and we describe how this system can be modified to obtain a 2HAM system that finitely self-assembles one of any fractal from an infinite set of fractals which we call 4-sided fractals. The 2HAM systems we give in this paper are the first examples of systems that finitely self-assemble discrete self-similar fractals at scale factor 1 in a purely growth model of self-assembly. Finally, we show that there exists a 3-sided fractal (which is not a tree fractal) that cannot be finitely self-assembled by any 2HAM system [1].
Definitions
4-sided fractal - any fractal whose generator fully contains the bounding rectangle of the generator.
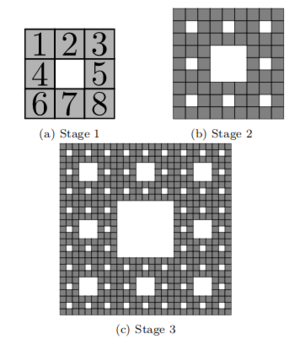
Sierpinski carpet - this fractal can be constructed by starting with a square, subdividing the square into nine congruent squares, removing the central square, and repeating this process on the eight remaining subsquares.
Overview
Fractals are mathematically interesting partially due to their complex self-similar structure. Fractals in nature often arrive at this structure through a series of local interactions motivated by simple rules; a process uniquely suited to simulation in self-assembly systems. The aTAM has been demonstrated to lack the ability to construct certain fractals and it is possible that the ATAM is unable to construct any non-trivial fractals. In previous work the 2HAM has been shown to be able to construct the Sierpinski carpet at temperature 2 with scale factor 3 [2] but this paper demonstrates that the 2HAM is able to self-assemble the Sierpinski carpet with scale factor 1. The paper also demonstrates that the 2HAM is capable of assembling any fractal at temperature 2 with scale factor 3 as long as that factor belongs to the special class of 4-sided fractals. It further shows that the 2HAM is unable to assemble a particular 3-sided fractal.
Results
The authors begin by demonstrating that the Sierpinski carpet can be assembled by the 2HAM at temperature 2 and scale factor 1. The tileset that accomplishes this task is made of initializer tiles and grout tiles. The initializer tiles are hardcoded to create 'stage 2' carpet supertiles.
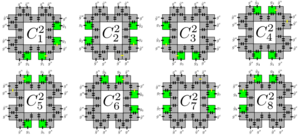
The grout tiles then assemble the stage 2 carpets into higher order carpets by building infrastructure between them to order their assembly. The grout tiles maintain the order of the surrounding supertiles by having eight copies of each grout tile corresponding to which corner of the next stage of assembly the supertile belongs to.
The same essential ideas are used to build tilesets that assemble any 4-sided fractal. The indicator tiles are relatively simple, being a hardcoded version of the original generator shape with the outer edges having specially defined glues to interact with the grout. The grout is similarly simple in that the grout fills the same purpose in the same way, but is altered to be long enough to span the width and height of the new generator shape.
Finally the paper concludes by proving that the following 3-sided fractal cannot be assembled by any tileset in the 2HAM.
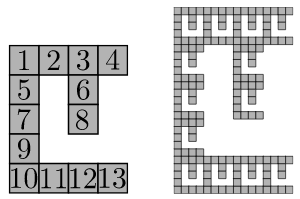
The proof showing this construction is impossible uses the pigeonhole principle in a way similar to the proof that the Sierpinski triangle cannot be assembled by any tileset in the aTAM. In essence, the shape possesses a natural 'bottleneck' that, as the shape propagates to larger constructions, guarantees that multiple possible legal constructions exist.
Further Work
The authors suggested that the presence of a Hamiltonian cycle and that the northernmost, southernmost, easternmost, and westernmost points of the fractal's generator each contain at least two distinct points might define a more general class of fractals that can be assembled by the 2HAM.