Geometric Hindrance
Revision as of 14:06, 2 July 2019 by \('"2\)'"7
Overview
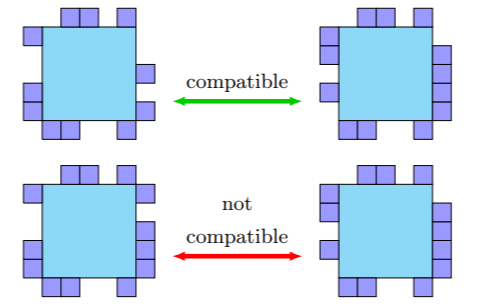
Geometric hindrance uses tile geometry to provide additional selection for which tiles may attach beyond glue labels. Tiles or tile assemblies that would overlap in at least some space are not allowed to bind. Models such as the geometric tile assembly model (GTAM) [1] [2] and polygon free-body tile assembly model (pfbTAM) [3] rely on tiles with geometries along each tile face. Other models such as the two-handed assembly model (2HAM) use the shape of the assemblies to select which two assemblies combine into one new assembly. The two-handed geometric tile assembly model (2GAM) combines the GTAM and 2HAM to further restrict which two assemblies can bind into one larger assembly. [1]
References
- ↑ 1.0 1.1
Bin Fu, Matthew J. Patitz, Robert T. Schweller, Bobby Sheline - Self-Assembly with Geometric Tiles
- ↑
Daniel Hader, Matthew J. Patitz - Geometric Tiles and Powers and Limitations of Geometric Hindrance in Self-Assembly
- ↑
Erik D. Demaine, Martin L. Demaine, Sándor P. Fekete, Matthew J. Patitz, Robert T. Schweller, Andrew Winslow, Damien Woods - One Tile to Rule Them All: Simulating Any Turing Machine, Tile Assembly System, or Tiling System with a Single Puzzle Piece