Nubots

Informal Description of the Model

The Nubot model was developed to capture some of the dynamics present in living biological systems. Particularly, the goal was to capture, among other things, the exponential growth that occurs in the human zygote, wherein a small number of cells with the same set of instructions can differentiate into the roughly \(10^{14}\) cells which make up a human. The model consists of a number of individual nubots which sit on the vertices of a triangular grid. Each nubot, depending on the configuration and states of its neighbors can perform a number of transitions which can consist of changing state, attaching to a neighbor, detaching from a neighbor, creating a new neighbor, removing a neighbor, or moving to an adjacent position. This model can also be subject to agitation, simulating Brownian motion or other such phenomena, which can cause nubots to non-deterministically move given that they are not already fixed in place through bonds.

Formal Definition of the Model

Let \(\mathbb{T}\) be the triangular lattice. A nubot monomer is a pair \((s, \vec{p})\) where \(s\in\Sigma\) is one of a finite set of states and \(\vec{p}\in\mathbb{T}\). Two neighboring monomers, ones residing on adjacent points in \(\mathbb{T}\), can be connected by rigid or flexible bonds or may not be connected at all. A connected component is a maximal set of neighboring monomers such that a path of bonds, rigid or flexible, exists between each pair of monomers in the set. A configuration is a finite set of monomers and the bonds between them.

Two neighboring monomers can interact by an interaction rule, \(r=(s_1, s_2, b, \vec{u})\to(s_1', s_2', b', \vec{u}')\) where \(s_1,s_2,s_1',s_2'\in\Sigma\cup\emptyset\) are monomer states, at most one of \(s_1\) or \(s_2\) are empty, \(b,b'\in\{\)flexible, rigid, \(\emptyset\}\) are bond types, and \(\vec{u},\vec{u}'\) are unit vectors in \(\mathbb{T}\) describing the relative position of the second monomer to the first before and after the interaction. Using these rules, we can cause monomers to change state, change bonds, move, appear, and disappear depending on the state of a neighboring monomer. When a monomer moves, the orientation of rigid bonds are preserved so that monomer will pull any monomers that are attached to it by a rigid bond. Flexible bonds can change orientation so long as the connected monomers stay within a unit distance after a move, otherwise they pull or push like rigid bonds.

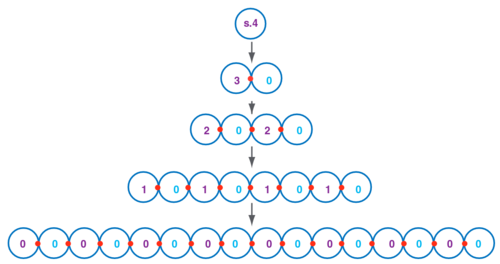
Controlled Exponential Growth

An overview of the parallel process by which nubots can grow in an exponentially long line.

The nubots model was designed to emulate the exponential behavior of cell division and other such natural processes. Because each nubot monomer performs its interaction rules in parallel with the other monomers, controlled exponential growth is achievable. To grow an exponentially long line, each monomer can grow a new monomer. Using bond change rules and movement rules, these new monomers can be moved in between the old monomers, effectively doubling the size of the line. By repeating this process, exponential growth can be achieved and by changing the states of the monomers after each phase, this growth can be controlled to stop after a fixed number of phases.

This process can even be used to facilitate the growth of larger, more complicated structures like squares very efficiently. Squares of size \(n\times n\) can be constructed in time \(O(\log{n})\) through the use of exponential line growth in both the \(x\) and \(y\) dimensions. Even arbitrary shapes can be made in time \(O(\log^2(n)\cdot t(|n|))\) where \(t(|n|)\) is the time required for a Turing machine to compute whether a pixel is in the shape or not using this parallel growth paradigm.

Other Results

By taking advantage of agitation, the number of states needed to construct shapes can also be drastically reduced. Squares of size \(n\times n\), for example, can be constructed using only a constant number of states with only a moderate slowdown to \(O(\log^2(n))\) expected time using agitation. This is done by letting agitation push components into their proper orientations and then locking the shape with rigid bonds once the components are properly placed.

In addition to building shapes, it is also possible to build binary counters and even simulate Turing machines in the nubots model. This shows that the nubots model is Turing universal.