Synchronous Tile Assembly Model (syncTAM)

The aTAM is meant to be a simplified mathematical model of tile-based self-assembly, and therefore it uses many simplifying assumptions. One of these is that the assembly process is broken into discrete steps, during each of which a single tile attaches to a growing assembly. Although it is unlikely that two tiles would attach to an assembly at exactly the same instant, as an assembly becomes larger and larger, more and more nearly simultaneous tile attachments will occur. This frequency would also increase in physically implemented systems if the concentrations of the free tiles were increased. In order to examine the end of the spectrum opposite from the aTAM, the synchronous Tile Assembly Model, in which arbitrary numbers of tiles may attach during a single step, was introduced.

Model Definition

The definition of the synchronous Tile Assembly Model (syncTAM) is nearly identical the aTAM, differing only in the number of tiles that attach during each step of assembly. As in the aTAM, the set of locations adjacent to the perimeter of an assembly into which tiles can validly bind is called the growth frontier, or simply the frontier, of the assembly. While the aTAM requires that at each step of assembly a single frontier location is selected at random to receive a tile, in the synchronous Tile Assembly Model (syncTAM), it is required that at each step of assembly every frontier location receives a tile. As the frontier of a system can grow arbitrarily large, the number of tiles added per assembly step may also grow arbitrarily large. As in the aTAM, if any single frontier location allows for \(\tau\)-strength binding of tiles of multiple types, one of those types is non-deterministically chosen for each such location. All other definitions and dynamics of the synTAM are similar to those of the aTAM.

Survey of Results

The reduced nondeterminism of the syncTAM allow it more power in some respects, e.g. universal computation at \(\tau=1\) and the ability to make certain shapes in a directed manner. However, it also provides restrictions that prevent any syncTAM system from making the full variety of shapes that many aTAM systems can (nondeterministically) generate. Following is a brief overview of some of these results.

Temperature-1 computation

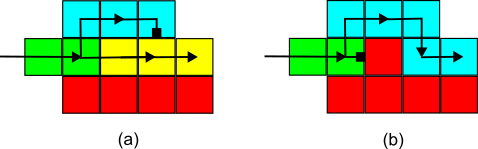
Universal computation is possible in the syncTAM since it is possible to make a bit-reader gadget. The general idea of a temperature-1 bit-reader is that it provides a mechanism for growth of a subset of tiles to be influenced by information from two separate previously-grown areas of an assembly in such a way that the resulting growth can be unique for each combination of bit values represented by those two areas. In the temperature-1 syncTAM this occurs with a single-tile-wide path of tiles growing from one of the input bits (and thus the glue value encodes the value of that bit). Then, that path grows across an area in which the second input bit was encoded by the presence or lack of a bump tile placed by the other region providing input. The path splits into two paths in such a way that: (1) if the bump does not exist, the lower path always succeeds in growth, and (2) if the bump does exist, the upper path always succeeds in growth. (The figure below depicts this.) The guaranteed success of exactly one path is due to the deterministic nature of the syncTAM that requires both paths to grow at every step unless geometrically blocked. In the aTAM, such a construction would not work because it would also be possible for the top path to just nondeterministically grow faster than the bottom path and, even if the bump doesn't exist, for the top path to beat the bottom path and thus represent incorrect information about the input region.

In such a way, whichever path successfully grows past the bump region is able to encode information about both input bits, and using such a gadget throughout the construction, it is possible for a syncTAM system to simulate an arbitrary Turing machine.

A bit-reading gadget in the temperature-1 syncTAM.

Shapes requiring synchronization

An infinite set of shapes can only be deterministically self-assembled in the syncTAM due to the strict control of tile additions that it provides. The figure below demonstrates one such shape. The seed is placed at the central bottom location, then the green and orange (resp.) paths grow diagonally upward and leftward and rightward (resp.). At each fourth upward step in diagonal growth, those paths initiate rows that grow inward toward the center. The green path initiates a red row that grows to the right, and the orange path initiates a blue row that grows to the left. Each such row grows a bump tile in each fourth location as well (with the red facing upward and the blue downward). As the pairs of rows meet each other near the center, the bump of one blocks further growth of the other. The consistent, deterministic speed of growth of each row and the guarantee that each bump will grow immediately allows for the shape depicted to deterministically grow in the syncTAM. However, in the aTAM the nondeterministic order of attachment of tiles in frontier locations leads to variable growth rates of arms and placements of bumps so that rows would not always collide and halt growth in the same, central location, and an infinite variety of shapes is produced by any aTAM system attempting to grow this shape.

An example shape that requires the synchronization of the syncTAM to self-assemble. Any system trying to self-assemble such a shape in the aTAM would also have to produce many non-target shapes.

aTAM systems that cannot be shape matched in the syncTAM

In the inverse of the previous result, the next result leverages the asynchronous nature of the aTAM to allow for an individual aTAM system to form an infinite set of shapes such that no system in the more constrained syncTAM can form all of those shapes. As schematically depicted by the figure below, the system grows one row rightward from the seed, potentially of infinite length. It also grows a row downward that can either continue downward to infinity or nondeterministically turn rightward at some point. If it does turn right, it grows exactly four tiles to the right and then grows upward. In the aTAM, such upward growth, despite how far down growth had previously gone, has some chance of beating the upper rightward growing row and blocking its growth. This is because, in the aTAM, growth of that row could have stalled for arbitrarily long while the bottom row was growing. However, in the syncTAM such stalling is not possible and the upper path must always win that competition, and therefore no syncTAM system can make all of shapes that such an aTAM system could. This result holds for any scale factor at which a syncTAM system attempts to make such shapes or positions of the seed tile.

A schematic depiction of an aTAM system that can form an infinite set of output shapes that cannot be matched by any single syncTAM system.