Difference between revisions of "Thermodynamic Binding Networks (TBN)"
(Added TBN page.) |
m (Changed spacing for aesthetic reasons.) |
||
| Line 1: | Line 1: | ||
[[Category:Self-assembly]] | [[Category:Self-assembly]] | ||
| − | |||
Thermodynamic Binding Network (TBN) is a model of molecular computing designed to incorporate the thermodynamic driving forces of enthalpy and entropy in order to ensure that the desired computational output is also the sole thermodynamic equilibrium. The system uses a simplified approach to the molecules themselves by presuming the monomers are unstructured collections of binding sites that are unconstrained by geometry. | Thermodynamic Binding Network (TBN) is a model of molecular computing designed to incorporate the thermodynamic driving forces of enthalpy and entropy in order to ensure that the desired computational output is also the sole thermodynamic equilibrium. The system uses a simplified approach to the molecules themselves by presuming the monomers are unstructured collections of binding sites that are unconstrained by geometry. | ||
A thermodynamic binding network (TBN) is a tuple $T = (D,M)$, where $D$ is the set of primary domain types. $D$ is mapped to a set of complementary domain types $D^*$ where $D^* = \{a^* | a \in D\}$. $M$ is then the set of monomer types, with each monomer type being a set(with the potential for repeated elements) in $N^{D \bigcup D^*}$, i.e. $\mathbf{m} \in M$, $\mathbf{m} = \{a,a,b,b^*\}$, $a,b \in D$. $T$ then has monomer collections that consist of some number of each monomer type, and these collections have various configurations corresponding to how the individual monomers bind and form polymers <ref name=thermo17/>. A monomer collection corresponds to a tile set in the aTAM, and form the basic unit of analysis in the study of TBNs. | A thermodynamic binding network (TBN) is a tuple $T = (D,M)$, where $D$ is the set of primary domain types. $D$ is mapped to a set of complementary domain types $D^*$ where $D^* = \{a^* | a \in D\}$. $M$ is then the set of monomer types, with each monomer type being a set(with the potential for repeated elements) in $N^{D \bigcup D^*}$, i.e. $\mathbf{m} \in M$, $\mathbf{m} = \{a,a,b,b^*\}$, $a,b \in D$. $T$ then has monomer collections that consist of some number of each monomer type, and these collections have various configurations corresponding to how the individual monomers bind and form polymers <ref name=thermo17/>. A monomer collection corresponds to a tile set in the aTAM, and form the basic unit of analysis in the study of TBNs. | ||
| − | |||
==Results in the TBN== | ==Results in the TBN== | ||
Revision as of 15:21, 14 June 2019
Thermodynamic Binding Network (TBN) is a model of molecular computing designed to incorporate the thermodynamic driving forces of enthalpy and entropy in order to ensure that the desired computational output is also the sole thermodynamic equilibrium. The system uses a simplified approach to the molecules themselves by presuming the monomers are unstructured collections of binding sites that are unconstrained by geometry.
A thermodynamic binding network (TBN) is a tuple \(T = (D,M)\), where \(D\) is the set of primary domain types. \(D\) is mapped to a set of complementary domain types \(D^*\) where \(D^* = \{a^* | a \in D\}\). \(M\) is then the set of monomer types, with each monomer type being a set(with the potential for repeated elements) in \(N^{D \bigcup D^*}\), i.e. \(\mathbf{m} \in M\), \(\mathbf{m} = \{a,a,b,b^*\}\), \(a,b \in D\). \(T\) then has monomer collections that consist of some number of each monomer type, and these collections have various configurations corresponding to how the individual monomers bind and form polymers [1]. A monomer collection corresponds to a tile set in the aTAM, and form the basic unit of analysis in the study of TBNs.
Results in the TBN
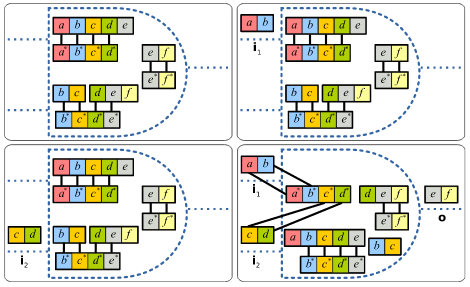
In the figure below there is an AND gate implemented as a strand-displacement model in the TBN. This AND gate implementation has been shown to remain stable when chained indefinitely, which allows the creation of arbitrary Boolean circuits in the TBN [1].
Any TBN \(T = (D,M)\) has been shown to have stable polymers of at most size exponential with respect to the number of domain types \(|D|\) and the number of polymer types \(|M|\) [1].
References
- ↑ 1.0 1.1 1.2
David Doty, Trent A. Rogers, David Soloveichik, Chris Thachuk, Damien Woods - Thermodynamic Binding Networks
- DNA Computing and Molecular Programming pp. 249--266,2017
- BibtexAuthor : David Doty, Trent A. Rogers, David Soloveichik, Chris Thachuk, Damien Woods
Title : Thermodynamic Binding Networks
In : DNA Computing and Molecular Programming -
Address :
Date : 2017