Difference between revisions of "Dupled abstract Tile Assembly Model (DaTAM)"
(Created page with "Dupled abstract Tile Assembly Model (DaTAM) is a slight extension to the abstract Tile Assembly Model (aTAM) that allows for not only the standard square tiles, but also “duple...") |
(Added references and a section on Computation) |
||
| Line 3: | Line 3: | ||
(i.e. square) tiles which are available for assembly, and $D$ is the set of duple tiles. The tile types which make up $S$ and $D$ all belong to $T$, with those in $D$ each being a combination of two tile types from $T$. | (i.e. square) tiles which are available for assembly, and $D$ is the set of duple tiles. The tile types which make up $S$ and $D$ all belong to $T$, with those in $D$ each being a combination of two tile types from $T$. | ||
| − | A dupled tile assembly system (DTAS) is a tuple $T = (T, S, D, \sigma, \tau )$, where $T$ is a finite tile set, $S \subseteq T$ is a finite set of singleton types, $D$ is a finite set of duple tile types, $\sigma: \mathcal{Z}^2 \longrightarrow T$is the finite, $\tau$-stable, seed assembly, and $\tau \in \mathcal{Z}^{+}$ is the temperature. | + | A dupled tile assembly system (DTAS) is a tuple $T = (T, S, D, \sigma, \tau )$, where $T$ is a finite tile set, $S \subseteq T$ is a finite set of singleton types, $D$ is a finite set of duple tile types, $\sigma: \mathcal{Z}^2 \longrightarrow T$is the finite, $\tau$-stable, seed assembly, and $\tau \in \mathcal{Z}^{+}$ is the temperature<ref name=duples14/>. |
| + | |||
| + | ==Universal Computation at Temperature 1== | ||
| + | |||
| + | In the [[Abstract Tile Assembly Model (aTAM)]], it has long been conjectured that universal computation is impossible at temperature 1; however, it has been shown that the DaTAM is capable universal computation at temperature 1<ref name=duples14 />. The proof for this is actually more general, showing that every for every compact [[Zig-Zag Systems|zig-zag system]] in the temperature 2 aTAM, there exists a temperature 1 DaTAM system which simulates it. When simulating a zig-zag system, because there is no cooperation at temperature 1 in the DaTAM, geometric bit reading gadgets are used to emulate cooperation in the aTAM by making use of the shape of duple tiles to detect which tile is being encoded on the row below. | ||
| + | |||
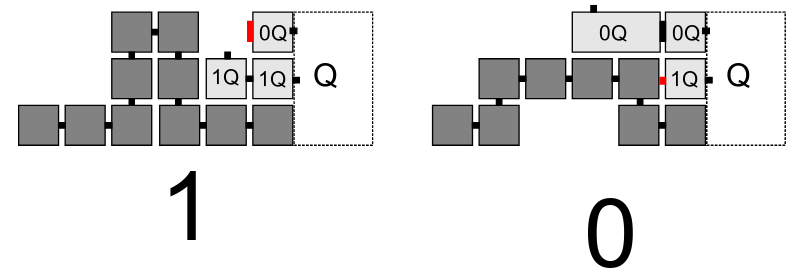
| + | [[File:Duple-bit-reading.png|frame|center|An illustration of a bit reading gadget which makes use of duple tiles. Notice that when encoding a 0, the tile 0Q can progress the assembly, whereas when encoding a 1, tile 1Q can progress the assembly]] | ||
| + | |||
| + | Since arbitrary Turing machines can be simulated using a zig-zag aTAM system at temperature 2, universal computation is possible in the DaTAM. | ||
| + | |||
| + | ==References== | ||
| + | <references> | ||
| + | |||
| + | <ref name=duples14><bibtex> | ||
| + | @INPROCEEDINGS{duples14, | ||
| + | author = "Jacob Hendricks and Matthew J. Patitz and Trent A. Rogers and Scott M. Summers", | ||
| + | title = "The Power of Duples (in Self-Assembly): It's Not So Hip To Be Square", | ||
| + | booktitle = "Lecture Notes in Computer Science", | ||
| + | volume = "8591", | ||
| + | series = "Computing and Combinatorics", | ||
| + | publisher = "Springer", | ||
| + | year = "2014", | ||
| + | } | ||
| + | </bibtex></ref> | ||
| + | |||
| + | </references> | ||
Revision as of 14:04, 31 May 2019
Dupled abstract Tile Assembly Model (DaTAM) is a slight extension to the abstract Tile Assembly Model (aTAM) that allows for not only the standard square tiles, but also “duple” tiles which are rectangles pre-formed by the joining of two square tiles. The addition of duples allows for powerful behaviors of self-assembling systems at temperature 1, meaning systems which exclude the requirement of cooperative binding by tiles (i.e., the requirement that a tile must be able to bind to at least 2 tiles in an existing assembly if it is to attach). The rectangular tiles are \(2 \times 1\) or \(1 \times 2\) rectangles which can logically be thought of as two square tiles which begin pre-attached to each other along an edge, hence the name duples. A dupled tile assembly system (DTAS) is an ordered 5-tuple \((T, S, D, \sigma, \tau )\) where \(T\), \(\sigma\), and \(\tau\) are as for a TAS, and S is the set of singleton (i.e. square) tiles which are available for assembly, and \(D\) is the set of duple tiles. The tile types which make up \(S\) and \(D\) all belong to \(T\), with those in \(D\) each being a combination of two tile types from \(T\).
A dupled tile assembly system (DTAS) is a tuple \(T = (T, S, D, \sigma, \tau )\), where \(T\) is a finite tile set, \(S \subseteq T\) is a finite set of singleton types, \(D\) is a finite set of duple tile types, \(\sigma: \mathcal{Z}^2 \longrightarrow T\)is the finite, \(\tau\)-stable, seed assembly, and \(\tau \in \mathcal{Z}^{+}\) is the temperature[1].
Universal Computation at Temperature 1
In the Abstract Tile Assembly Model (aTAM), it has long been conjectured that universal computation is impossible at temperature 1; however, it has been shown that the DaTAM is capable universal computation at temperature 1[1]. The proof for this is actually more general, showing that every for every compact zig-zag system in the temperature 2 aTAM, there exists a temperature 1 DaTAM system which simulates it. When simulating a zig-zag system, because there is no cooperation at temperature 1 in the DaTAM, geometric bit reading gadgets are used to emulate cooperation in the aTAM by making use of the shape of duple tiles to detect which tile is being encoded on the row below.
Since arbitrary Turing machines can be simulated using a zig-zag aTAM system at temperature 2, universal computation is possible in the DaTAM.