Sierpinski triangle in the kTAM

Introduction

The kinetic tile assembly model (kTAM) builds upon the abstract model (aTAM) by allowing not only for the binding of tiles, but also for the unbinding of tiles. At a high level you might think about the binding and unbinding in the kTAM as growth and decay, or more formally as association and dissociation. Further, the kTAM also allows for tiles to bind which have no matching glues. The binding allowances introduced in the kTAM are there to mimic the chemical behavior of DNA.

This tutorial will step you through the basic concepts of the kTAM. While working with the kTAM you will notice that there are trade-offs between speed of assembly and accuracy of assembly. For example, it is possible to have an assembly that builds very quickly to a given size, yet without proper tile types, the assembly will be filled with errors. The other undesirable alternative is to build very slowly but accurately. Fortunately, there is a middle path that we can take known broadly as error management. Error management within the kTAM involves recognizing the potential errors that can occur for a tile set and then redesigning that tile set so that it is more resilient to errors, still produces the expected output, and does so in a shorter period of time.

While experimenting with the kTAM using TAS we recommend adjusting the refresh rate of the assembly to between 1,000 and 10,000 and we also recommend turning off caching, or the saving of past tile placements.

Error types

There are three basic error types that can occur during assembly:

1. Growth (or Mismatch)
2. Facet
3. Nucleation

Growth Errors

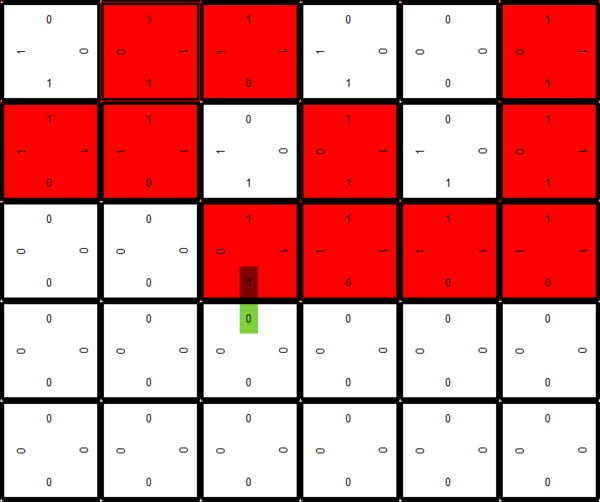
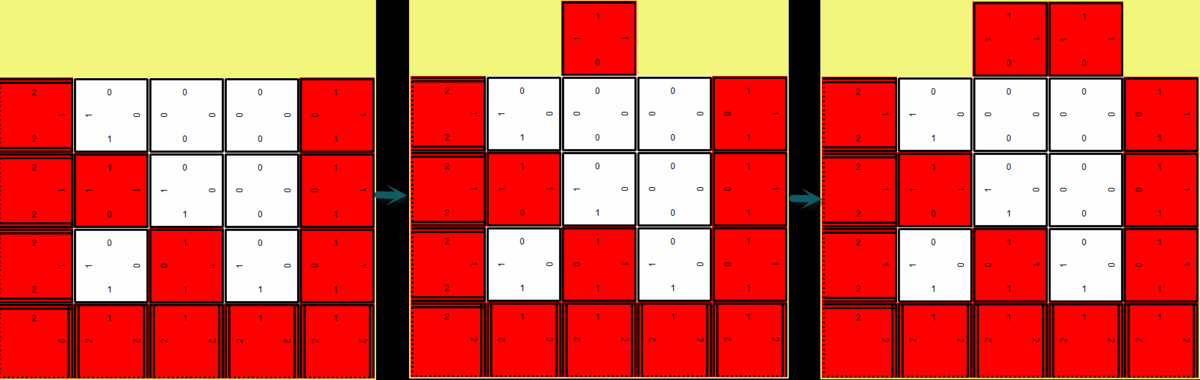
A growth error occurs when a tile binds to a frontier-tile but the adjacent glues of the respective binding edges do not match. The disassociation rate (Gse) within the kTAM dictates how long this mismatched edge will stay bound. The higher the Gse the longer the error can persist before unbinding. However, even with a normal ratio of Gmc/Gse it is still possible that the mismatched tiles will stay bound long enough for appropriately matched tiles to fill out the space around the error and permanently bind it into place. Once the anomaly is bound in place further deviations from the desired assembly shape may be propagated throughout the assembly. A visual example of this can be seen below in a 7-tile Sierpinski assembly. The top image is a zoomed in section of the assembly that shows the glue labels of each tile. Notice that under the green highlight there is a matching error between the respective tile edges. The same assembly is shown in the second image but zoomed out. The green mark represents the only binding error in the entire assembly, but as can be seen, it ruined the expected periodicity of the assembly.

Growth error.

Growth error, zoomed out.

Facet Errors

Facet errors, like growth errors, occur along the frontier of the assembly and between two tile edges which have insufficient strength to form a permanent attachment given the current Gmc/Gse. Facet errors become permanent when they are locked into place by subsequent tile addition. Unlike growth errors, however, facet errors are characterized by matching edges.

Nucleation Errors

A nucleation error occurs when tiles associate with each other outside of the seed structure and start another seeded structure.

Error Management within the kTAM

A common technique to reduce growth errors is called proofreading. With the proofreading method individual type types are replaced by n X n blocks of unique tile types such that the perimeter of the n X n block formed by them represents the same glues as the original tile.