Difference between revisions of "Synchronous Tile Assembly Model (syncTAM)"
| Line 10: | Line 10: | ||
The reduced nondeterminism of the syncTAM allow it more power in some respects, e.g. universal computation at $\tau=1$ and the ability to make certain shapes in a directed manner. However, it also provides restrictions that prevent any syncTAM system from making the full variety of shapes that many aTAM systems can (nondeterministically) generate. | The reduced nondeterminism of the syncTAM allow it more power in some respects, e.g. universal computation at $\tau=1$ and the ability to make certain shapes in a directed manner. However, it also provides restrictions that prevent any syncTAM system from making the full variety of shapes that many aTAM systems can (nondeterministically) generate. | ||
| − | + | ===Temperature-1 computation=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
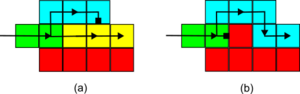
| − | + | Universal computation is possible in the syncTAM since it is possible to make a bit-reader gadget. [[File:SyncTAM_bit_reading_gadget.png|thumb|center|A bit-reading gadget in the temperature-1 syncTAM.]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ===Shapes requiring synchronization=== | ||
| + | |||
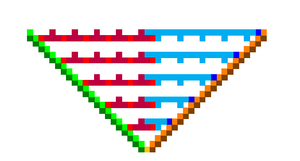
| + | An infinite set of shapes can only be deterministically self-assembled in the syncTAM due to the strict control of tile additions that it provides. [[File:SyncTAM_shape.png|thumb|center|An example shape that requires the synchronization of the syncTAM to self-assemble. Any system trying to self-assemble such a shape in the aTAM would also have to produce many non-target shapes.]] | ||
| + | |||
| + | ===aTAM systems that cannot be shape matched in the syncTAM=== | ||
| + | |||
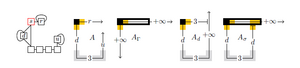
| + | The asynchronous nature of the aTAM allows for an individual aTAM system to potentially form an infinite set of shapes, but no system in the more constrained syncTAM can form all of those shapes. [[File:SyncTAM_imposs_shape.png|thumb|center|A schematic depiction of an aTAM system that can form an infinite set of output shapes that cannot be matched by any single syncTAM system.]] | ||
[[Category: Tile Assembly Models]] | [[Category: Tile Assembly Models]] | ||
[[Category:Self-assembly]] | [[Category:Self-assembly]] | ||
Revision as of 23:44, 19 April 2025
The aTAM is meant to be a simplified mathematical model of tile-based self-assembly, and therefore it uses many simplifying assumptions. One of these is that the assembly process is broken into discrete steps, during each of which a single tile attaches to a growing assembly. Although if time is assumed to be continuous it is unlikely that two tiles would attach to an assembly at exactly the same time, as an assembly becomes larger and larger, more and more nearly simultaneous tile attachments will occur. This frequency would also increase in physically implemented systems if the concentrations of the free tiles was increased. In order to examine the end of the spectrum opposite to the aTAM in which a single tile is allowed to attach in each time step, the synchronous Tile Assembly Model, in which arbitrary numbers of tiles may attach during a single step, was introduced.
Contents
Model Definition
In the aTAM, the set of locations adjacent to the perimeter of an assembly into which tiles can validly bind is called the growth frontier, or simply frontier, of the assembly. While the aTAM requires that at each step of assembly a single frontier location is selected at random to receive a tile, in the synchronous Tile Assembly Model (syncTAM), it is required that at each step of assembly every frontier location receives a tile. As the frontier of a system can grow arbitrarily large, the number of tiles added per assembly step may also grow arbitrarily large. As in the aTAM, if any single frontier location allows for \(\tau\)-strength binding of tiles of multiple types, one of those types is non-deterministically chosen for each such location.
Survey of Results
The reduced nondeterminism of the syncTAM allow it more power in some respects, e.g. universal computation at \(\tau=1\) and the ability to make certain shapes in a directed manner. However, it also provides restrictions that prevent any syncTAM system from making the full variety of shapes that many aTAM systems can (nondeterministically) generate.
Temperature-1 computation
Universal computation is possible in the syncTAM since it is possible to make a bit-reader gadget.
Shapes requiring synchronization
An infinite set of shapes can only be deterministically self-assembled in the syncTAM due to the strict control of tile additions that it provides.
aTAM systems that cannot be shape matched in the syncTAM
The asynchronous nature of the aTAM allows for an individual aTAM system to potentially form an infinite set of shapes, but no system in the more constrained syncTAM can form all of those shapes.