Blocked Tile Assembly Model (BlockTAM)

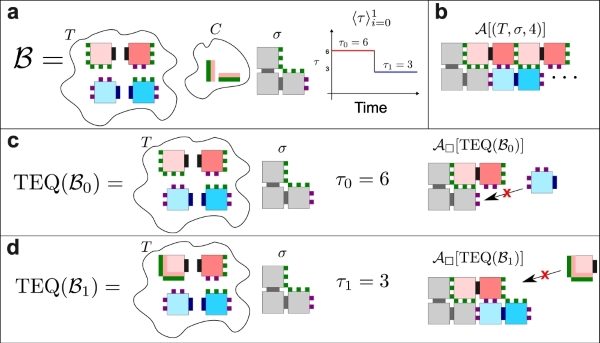
In tile-based models of self-assembly such as the aTAM, all input to a system is provided at the beginning of the process in the form of pre-made seed assemblies and copies of unbound tiles of a fixed set of tile types, and then self-assembly proceeds during the duration of a relatively constant temperature. The Blocked Tile Assembly Model, or BlockTAM, is a mathematical model of tile-based self-assembling systems that allows for additional dynamics and types of input to its systems. The major differences from the aTAM are that a series of temperatures can be specified so that the assembly process proceeds through each of them in sequence, and that so-called blockers, which are components that disable glues when the temperatures are in fixed ranges, can be included with systems. These changes allow for a notable increase in the possible dynamics for BlackTAM systems.

Model Definition

The definition of the Block Tile Assembly Model (BlockTAM) is similar to the multiple temperature model...

This page is currently under construction, and more content is coming soon!

Example BlockTAM system

The following figure shows an example of a BlockTAM system.

An example BlockTAM system.

TBD: Add a description.

Survey of Results

Initial results in the BlockTAM have shown how so-called universal tile sets can be designed for certain tasks, such as encoding numbers or making assemblies of given shapes, so that the only input specified to them is provided via a series of temperature changes. Those temperature changes are used to drive the self-assembly processes of BlockTAM systems to achieve the specified tasks. Following is a brief overview of some of these results.

Universal number encoding

For any set of temperatures of size \(\ge 3\) there exists a universal number encoder which is a tile set, cover set, and seed tile such that, for any given input number \(n\), a temperature sequence (over the given set of temperatures) exists such that the resulting BlockTAM system is directed and the unique terminal assembly is a rectangle such that the number \(n\) is encoded in the glues on the north of the assembly. (The base and format of the encoding is dependent upon the size of the temperature set that the universal number encoder was built for.)

Base 10 number 100 encoded by the universal number encoder for temperatures 2,3,4

Universal shape building

TBD: give an overview of this construction...

An example shape that requires the synchronization of the syncTAM to self-assemble. Any system trying to self-assemble such a shape in the aTAM would also have to produce many non-target shapes.

Examples and Simulation Software

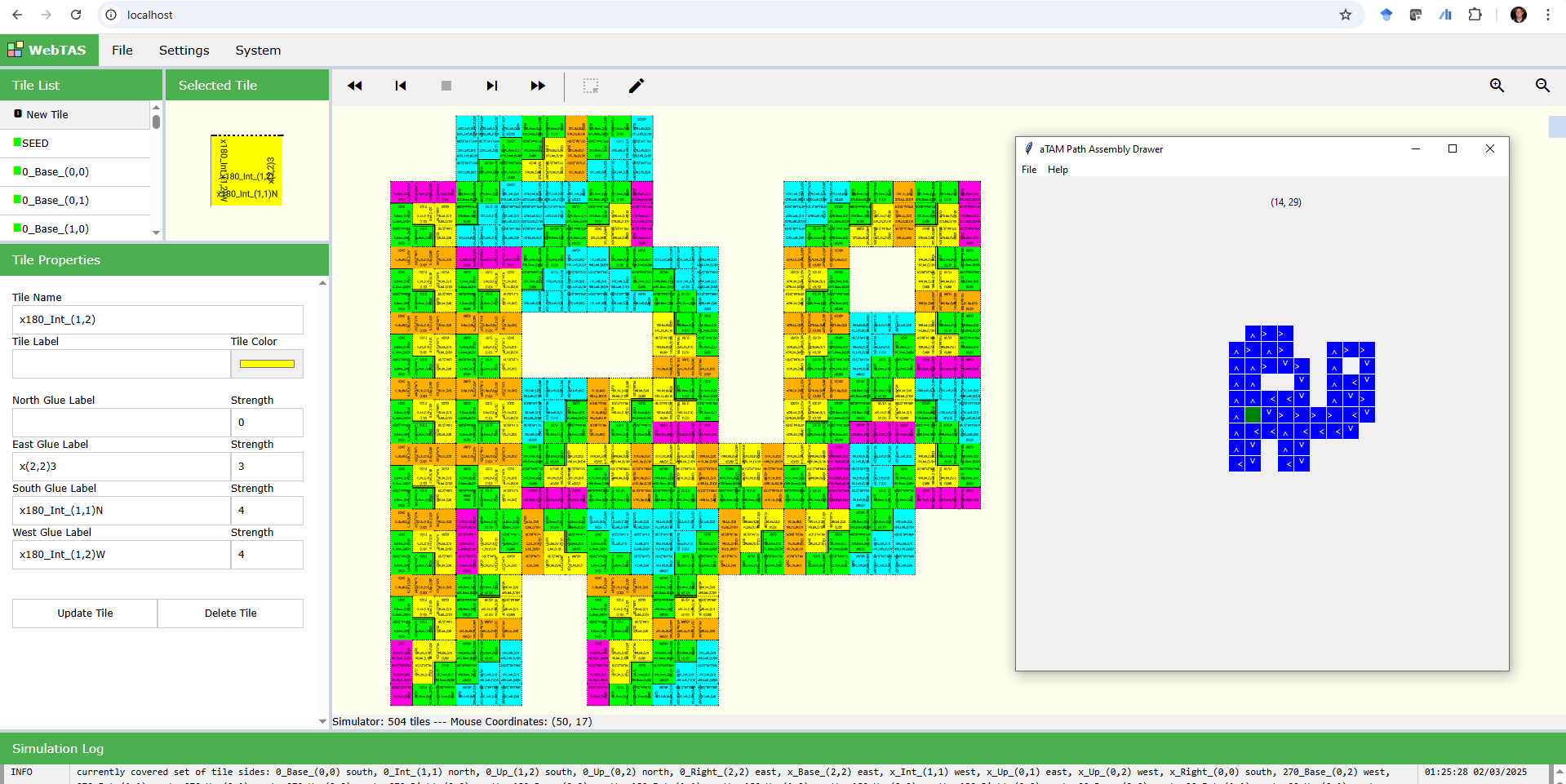
The BlockTAM can be simulated by (the currently beta version of) | WebTAS. However, note there are a few caveats:

• WebTAS supports two slight variations of the model, and the version that matches that defined in the DNA31 submission is called 'version 2' in WebTAS (and the scripts included in this package).
• WebTAS can load and run BlockTAM systems, but does not yet support creation, editing, or saving of BlockTAM systems.

In the downloadable package linked below is a Python script allowing one to draw a path and save it as a BlockTAM system utilizing the universal shape builder construction, which can then be simulated in WebTAS. The following image shows the path drawing software on the right and the simulated system to its left.

An example shape drawn in the BlockTAM Path Drawer and them simulated in WebTAS

Examples of systems cited above, as well as scripts for generating universal number encoders, universal shape builders, and the temperature sequences used to control them can be downloaded from | BlockTAM_examples. (Clicking on the most recent, bottommost link will download a zip file containing the files.)