Difference between revisions of "Synchronous Tile Assembly Model (syncTAM)"
| Line 1: | Line 1: | ||
| − | The [[Abstract Tile Assembly Model (aTAM) | aTAM]] is meant to be a simplified mathematical model of tile-based self-assembly, and therefore it uses many simplifying assumptions. One of these is that the assembly process is broken into discrete steps, during each of which a single tile attaches to a growing assembly. Although | + | The [[Abstract Tile Assembly Model (aTAM) | aTAM]] is meant to be a simplified mathematical model of tile-based self-assembly, and therefore it uses many simplifying assumptions. One of these is that the assembly process is broken into discrete steps, during each of which a single tile attaches to a growing assembly. Although it is unlikely that two tiles would attach to an assembly at exactly the same instant, as an assembly becomes larger and larger, more and more nearly simultaneous tile attachments will occur. This frequency would also increase in physically implemented systems if the concentrations of the free tiles were increased. In order to examine the end of the spectrum opposite from the aTAM, the synchronous Tile Assembly Model, in which arbitrary numbers of tiles may attach during a single step, was introduced. |
__TOC__ | __TOC__ | ||
==Model Definition== | ==Model Definition== | ||
| − | + | The definition of the synchronous Tile Assembly Model (syncTAM) is nearly identical the [[Abstract Tile Assembly Model (aTAM) | aTAM]], differing only in the number of tiles that attach during each step of assembly. As in the aTAM, the set of locations adjacent to the perimeter of an assembly into which tiles can validly bind is called the [[Growth Frontier | growth frontier]], or simply the frontier, of the assembly. While the aTAM requires that at each step of assembly a single frontier location is selected at random to receive a tile, in the synchronous Tile Assembly Model (syncTAM), it is required that at each step of assembly ''every'' frontier location receives a tile. As the frontier of a system can grow arbitrarily large, the number of tiles added per assembly step may also grow arbitrarily large. As in the aTAM, if any single frontier location allows for $\tau$-strength binding of tiles of multiple types, one of those types is non-deterministically chosen for each such location. All other definitions and dynamics of the synTAM are similar to those of the aTAM. | |
==Survey of Results== | ==Survey of Results== | ||
| − | The reduced nondeterminism of the syncTAM allow it more power in some respects, e.g. universal computation at $\tau=1$ and the ability to make certain shapes in a directed manner. However, it also provides restrictions that prevent any syncTAM system from making the full variety of shapes that many aTAM systems can (nondeterministically) generate. | + | The reduced nondeterminism of the syncTAM allow it more power in some respects, e.g. universal computation at $\tau=1$ and the ability to make certain shapes in a directed manner. However, it also provides restrictions that prevent any syncTAM system from making the full variety of shapes that many aTAM systems can (nondeterministically) generate. Following is a brief overview of some of these results. |
===Temperature-1 computation=== | ===Temperature-1 computation=== | ||
Revision as of 07:56, 20 April 2025
The aTAM is meant to be a simplified mathematical model of tile-based self-assembly, and therefore it uses many simplifying assumptions. One of these is that the assembly process is broken into discrete steps, during each of which a single tile attaches to a growing assembly. Although it is unlikely that two tiles would attach to an assembly at exactly the same instant, as an assembly becomes larger and larger, more and more nearly simultaneous tile attachments will occur. This frequency would also increase in physically implemented systems if the concentrations of the free tiles were increased. In order to examine the end of the spectrum opposite from the aTAM, the synchronous Tile Assembly Model, in which arbitrary numbers of tiles may attach during a single step, was introduced.
Contents
Model Definition
The definition of the synchronous Tile Assembly Model (syncTAM) is nearly identical the aTAM, differing only in the number of tiles that attach during each step of assembly. As in the aTAM, the set of locations adjacent to the perimeter of an assembly into which tiles can validly bind is called the growth frontier, or simply the frontier, of the assembly. While the aTAM requires that at each step of assembly a single frontier location is selected at random to receive a tile, in the synchronous Tile Assembly Model (syncTAM), it is required that at each step of assembly every frontier location receives a tile. As the frontier of a system can grow arbitrarily large, the number of tiles added per assembly step may also grow arbitrarily large. As in the aTAM, if any single frontier location allows for \(\tau\)-strength binding of tiles of multiple types, one of those types is non-deterministically chosen for each such location. All other definitions and dynamics of the synTAM are similar to those of the aTAM.
Survey of Results
The reduced nondeterminism of the syncTAM allow it more power in some respects, e.g. universal computation at \(\tau=1\) and the ability to make certain shapes in a directed manner. However, it also provides restrictions that prevent any syncTAM system from making the full variety of shapes that many aTAM systems can (nondeterministically) generate. Following is a brief overview of some of these results.
Temperature-1 computation
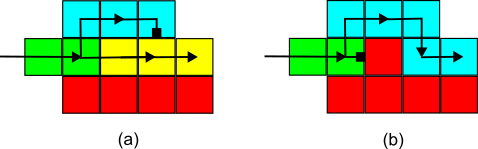
Universal computation is possible in the syncTAM since it is possible to make a bit-reader gadget.
Shapes requiring synchronization
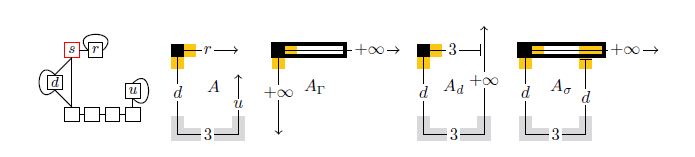
An infinite set of shapes can only be deterministically self-assembled in the syncTAM due to the strict control of tile additions that it provides.
aTAM systems that cannot be shape matched in the syncTAM
The asynchronous nature of the aTAM allows for an individual aTAM system to potentially form an infinite set of shapes, but no system in the more constrained syncTAM can form all of those shapes.