Difference between revisions of "Synchronous Tile Assembly Model (syncTAM)"
(Created page with "The aTAM is meant to be a simplified mathematical model of tile-based self-assembly, and therefore it uses many simplifying assumptio...") |
|||
| Line 1: | Line 1: | ||
| − | The [[Abstract Tile Assembly Model (aTAM) | aTAM]] is meant to be a simplified mathematical model of tile-based self-assembly, and therefore it uses many simplifying assumptions. One of these is that | + | The [[Abstract Tile Assembly Model (aTAM) | aTAM]] is meant to be a simplified mathematical model of tile-based self-assembly, and therefore it uses many simplifying assumptions. One of these is that the assembly process is broken into discrete steps, during each of which a single tile attaches to a growing assembly. Although if time is assumed to be continuous it is unlikely that two tiles would attach to an assembly at exactly the same time, as an assembly becomes larger and larger, more and more nearly simultaneous tile attachments will occur. This frequency would also increase in physically implemented systems if the concentrations of the free tiles was increased. In order to examine the end of the spectrum opposite to the aTAM in which a single tile is allowed to attach in each time step, the synchronous Tile Assembly Model, in which arbitrary numbers of tiles may attach during a single step, was introduced. |
__TOC__ | __TOC__ | ||
==Model Definition== | ==Model Definition== | ||
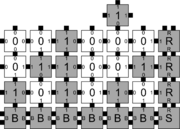
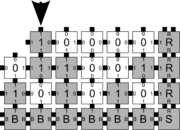
| − | In the syncTAM, ... | + | In the [[Abstract Tile Assembly Model (aTAM) | aTAM]], the set of locations adjacent to the perimeter of an assembly into which tiles can validly bind is called the [[Growth Frontier | growth frontier]], or simply frontier, of the assembly. While the aTAM requires that at each step of assembly a single frontier location is selected at random to receive a tile, in the synchronous Tile Assembly Model (syncTAM), it is required that at each step of assembly ''every'' frontier location receives a tile. As the frontier of a system can grow arbitrarily large, the number of tiles added per assembly step may also grow arbitrarily large. As in the aTAM, if any single frontier location allows for $\tau$-strength binding of tiles of multiple types, one of those types is non-deterministically chosen for each such location. |
| + | |||
| + | ==Survey of Results== | ||
| + | The ability of the kTAM to accurately model the errors seen in laboratory settings coupled with its clean theoretical definition make it an ideal model in which to study mechanisms of error prevention and correction. Additionally, the algorithmic nature of self-assembly in the kTAM provides the opportunity to effectively apply a variety of algorithms from seemingly unrelated fields such as data transmission to make kTAM systems more robust. | ||
{{multiple image | {{multiple image | ||
| Line 40: | Line 43: | ||
<br> | <br> | ||
<br> | <br> | ||
| − | |||
| − | |||
| − | |||
Revision as of 01:05, 19 April 2025
The aTAM is meant to be a simplified mathematical model of tile-based self-assembly, and therefore it uses many simplifying assumptions. One of these is that the assembly process is broken into discrete steps, during each of which a single tile attaches to a growing assembly. Although if time is assumed to be continuous it is unlikely that two tiles would attach to an assembly at exactly the same time, as an assembly becomes larger and larger, more and more nearly simultaneous tile attachments will occur. This frequency would also increase in physically implemented systems if the concentrations of the free tiles was increased. In order to examine the end of the spectrum opposite to the aTAM in which a single tile is allowed to attach in each time step, the synchronous Tile Assembly Model, in which arbitrary numbers of tiles may attach during a single step, was introduced.
Contents
Model Definition
In the aTAM, the set of locations adjacent to the perimeter of an assembly into which tiles can validly bind is called the growth frontier, or simply frontier, of the assembly. While the aTAM requires that at each step of assembly a single frontier location is selected at random to receive a tile, in the synchronous Tile Assembly Model (syncTAM), it is required that at each step of assembly every frontier location receives a tile. As the frontier of a system can grow arbitrarily large, the number of tiles added per assembly step may also grow arbitrarily large. As in the aTAM, if any single frontier location allows for \(\tau\)-strength binding of tiles of multiple types, one of those types is non-deterministically chosen for each such location.
Survey of Results
The ability of the kTAM to accurately model the errors seen in laboratory settings coupled with its clean theoretical definition make it an ideal model in which to study mechanisms of error prevention and correction. Additionally, the algorithmic nature of self-assembly in the kTAM provides the opportunity to effectively apply a variety of algorithms from seemingly unrelated fields such as data transmission to make kTAM systems more robust.