Difference between revisions of "Signal-passing Tile Assembly Model (STAM)"
(Terminal assemblies) |
|||
| (5 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | The Signal-passing Tile Assembly (STAM)<ref name="JMRSNR" /> is an asynchronous model of tile self-assembly which is considered as an extension of the 2-Handed Assembly Model ([[Two-Handed Assembly Model (2HAM)|2HAM]])<ref name="AGKS05g" /> and is based on active glues which can dynamically change state, allowing any action of turning a glue <tt>on</tt> or <tt>off</tt>, attaching a new tile, or breaking apart an assembly to happen in any order.In STAM basic tiles of the Tile Assembly Model ([[Tile Assembly Model|TAM]]) are augmented with the ability to receive information, in the form of signals, from neighboring tiles in an assembly, and to pass signals to neighboring tiles. A very important feature of signals is that each signal can only move across any given tile one time - they are not reusable <ref name="JEWKNC" />. | + | The Signal-passing Tile Assembly Model (STAM)<ref name="JMRSNR" /> is an asynchronous model of tile self-assembly which is considered as an extension of the 2-Handed Assembly Model ([[Two-Handed Assembly Model (2HAM)|2HAM]])<ref name="AGKS05g" /> and is based on active glues which can dynamically change state, allowing any action of turning a glue <tt>on</tt> or <tt>off</tt>, attaching a new tile, or breaking apart an assembly to happen in any order.In STAM basic tiles of the Tile Assembly Model ([[Tile Assembly Model|TAM]]) are augmented with the ability to receive information, in the form of signals, from neighboring tiles in an assembly, and to pass signals to neighboring tiles. A very important feature of signals is that each signal can only move across any given tile one time - they are not reusable <ref name="JEWKNC" />. |
Generalized model of STAM imposes minimal restrictions on aspects such as the speed of signals and orderings of events. This generalized version, while perhaps difficult to create well-behaved constructions within, provides a framework that is intended to be maximally independent of the specific details of potential physical implementations of actual signal tiles and enriches the tile assembly paradigm with greater capabilities that anticipate advancing techniques in the field of DNA nanotechnology and allow tile assembly to more closely emulate biological and natural processes.<ref name="JEWKNC" /> | Generalized model of STAM imposes minimal restrictions on aspects such as the speed of signals and orderings of events. This generalized version, while perhaps difficult to create well-behaved constructions within, provides a framework that is intended to be maximally independent of the specific details of potential physical implementations of actual signal tiles and enriches the tile assembly paradigm with greater capabilities that anticipate advancing techniques in the field of DNA nanotechnology and allow tile assembly to more closely emulate biological and natural processes.<ref name="JEWKNC" /> | ||
| Line 26: | Line 26: | ||
#turn that glue off (valid if it is currently on or latent). | #turn that glue off (valid if it is currently on or latent). | ||
| − | Note that turning a glue off breaks any bond that that glue may have formed with a neighboring tile. The transition function defined for each tile type is allowed a unique set of output actions for the binding event of each glue along its edges. As the STAM is an extension of the [[Two-Handed Assembly Model (2HAM)|2HAM]], binding and breaking can occur between pairs of arbitrarily sized supertiles. In order to allow for physical mechanisms which implement the transition functions of tiles but are arbitrarily slower or faster than the average rates of (super)tile attachments and detachments, rather than immediately enacting the outputs of transition functions, each output action is put into a set of "pending actions" which includes all actions which have not yet been enacted for that glue. An STAM system consists of a set of tiles and a temperature value. To define what is producible from such a system, we use a recursive definition of producible assemblies which starts with the initial tiles and then contains any supertiles which can be formed by doing the following to any producible assembly: | + | This means that glues can only be <tt>on</tt> once (although may remain so for an arbitrary amount of time or permanently), either by starting in that state or being switched on from latent, and if they are ever switched to off then no further transitions are allowed for that glue. This essentially provides a single “use” of a glue (and thus the implicit signal sent by its activation and binding). Note that turning a glue off breaks any bond that that glue may have formed with a neighboring tile. The transition function defined for each tile type is allowed a unique set of output actions for the binding event of each glue along its edges. As the STAM is an extension of the [[Two-Handed Assembly Model (2HAM)|2HAM]], binding and breaking can occur between pairs of arbitrarily sized supertiles. In order to allow for physical mechanisms which implement the transition functions of tiles but are arbitrarily slower or faster than the average rates of (super)tile attachments and detachments, rather than immediately enacting the outputs of transition functions, each output action is put into a set of "pending actions" which includes all actions which have not yet been enacted for that glue. An STAM system consists of a set of tiles and a temperature value. To define what is producible from such a system, we use a recursive definition of producible assemblies which starts with the initial tiles and then contains any supertiles which can be formed by doing the following to any producible assembly: |
#executing any entry from the pending actions of any one glue within a tile within that supertile (and then that action is removed from the pending set), | #executing any entry from the pending actions of any one glue within a tile within that supertile (and then that action is removed from the pending set), | ||
| − | # binding with another supertile if they are able for form a $\tau$-stable supertile, or | + | #binding with another supertile if they are able for form a $\tau$-stable supertile, or |
| + | #breaking apart into 2 separate supertiles along a cut whose total strength is less than $\tau$. | ||
| + | As an overview, tiles in the STAM pass signals to neighboring tiles simply by activating glues which can bind with glues on adjacent edges of neighboring tiles. The information content of a signal is dependent upon the transition function of the receiving tile, that is, by what glue actions the receiving tile initiates upon the binding of its glue. By subsequently activating and deactivating its own glues, the receiving tile can propagate the signal to any of its neighbors. Solely by utilizing the mechanism of glue activation and deactivation initiated and carried out on individual tiles but chained together through series of glue bindings, a global network which is capable of passing information across entire assemblies (and also of allowing them to selectively enable sites for further growth or to discard arbitrary portions of the assembly), is created. However, an important restriction is the ''fire once'' nature of the signals, meaning that each glue can only transition to any given state once, and therefore the number of signals which a tile can process is a constant dependent upon the definition of the tile type. | ||
| + | |||
| + | |||
| + | |||
| + | ===Formal Definition of the Signal Passing Tile Assembly Model=== | ||
'''Basic Notation''' | '''Basic Notation''' | ||
Let $D$ denote the set of labels $\{north, south, east, west\}$, or $\{N,S,E,W\}$. | Let $D$ denote the set of labels $\{north, south, east, west\}$, or $\{N,S,E,W\}$. | ||
| + | |||
'''Active Glues and Glue States''' | '''Active Glues and Glue States''' | ||
| Line 43: | Line 50: | ||
[[File:The_valid_state_transitions_for_active_glues.jpg|thumb|300px|Fig. 2: The valid state transitions for active glues | [[File:The_valid_state_transitions_for_active_glues.jpg|thumb|300px|Fig. 2: The valid state transitions for active glues | ||
Credit:Asynchronous Signal Passing for Tile Self-Assembly: Fuel Efficient Computation and Efficient Assembly of Shapes]] | Credit:Asynchronous Signal Passing for Tile Self-Assembly: Fuel Efficient Computation and Efficient Assembly of Shapes]] | ||
| − | |||
| Line 54: | Line 60: | ||
'''Active Tiles and Transition Functions''' | '''Active Tiles and Transition Functions''' | ||
| − | A ''generalized active tile type'' $t$ is a unit square defined as a $4$-tuple $t = \left(G, L, \delta, \Pi\right)$ where $G: D \rightarrow P(\Gamma \times Q)$ is a function specifying the set of all active glues present on a given side, $L$ is the set of all active labels, $\delta: D \times \Gamma \rightarrow P(((D \times \Gamma \times \{\texttt{on}, \texttt{off}\}) \cup (\Sigma \times \{\texttt{on}, \texttt{off}\}))$ is the | + | A ''generalized active tile type'' $t$ is a unit square defined as a $4$-tuple $t = \left(G, L, \delta, \Pi\right)$ where $G: D \rightarrow P(\Gamma \times Q)$ is a function specifying the set of all active glues present on a given side, $L$ is the set of all active labels, $\delta: D \times \Gamma \rightarrow P(((D \times \Gamma \times \{\texttt{on}, \texttt{off}\}) \cup (\Sigma \times \{\texttt{on}, \texttt{off}\}))$ is the ''transition function'' and $\Pi$ is a multiset over $(D \times \Gamma \times \{\texttt{on}, \texttt{off}\}) \cup (\Sigma \times \{\texttt{on}, \texttt{off}\})$. A generalized active tile type $t = (G, L, \delta, \Pi)$ is an ''active tile type'' if, for all $d \in D$ and for all active glues $(g,q),(g',q') \in G(d)$, $g \ne g'$. In other words, while a tile side may have multiple glues, there cannot be multiple copies of the same type of glue on a single side. |
| − | A transition function $\delta$ takes as input a direction $d \in D$ and a glue type $g \in \Gamma$ (i.e. we say that it is | + | A transition function $\delta$ takes as input a direction $d \in D$ and a glue type $g \in \Gamma$ (i.e. we say that it is ''fired'' by the binding of glue type $g$ on side $d$ of $t$), and outputs a (possibly empty) set of ''glue'' or ''label actions'', i.e., elements of $(D \times \Gamma \times \{\texttt{on}, \texttt{off}\}) \cup (\Sigma \times \{\texttt{on}, \texttt{off}\})$. Consider an active tile type $t = (G, L, \delta, \Pi)$ and suppose that $(g,q) \in G(d)$ for some $d \in D$ and $(d', g' ,q') \in \delta(d,g)$. Intuitively, if $m = \Pi(d', q')$ (i.e., the ''multiplicity'' of $(d',q') \in \Pi$) $before$ $\delta$ ''fires,'' then $\Pi(d', q') = m + 1$ ''after'' executing $\delta$. We assume for the sake of convenience that $\delta$ outputs the empty set for any pair of direction and glue on which $\delta$ is not explicitly defined. In other words, the binding of a glue on $t$ ''fires'' the transition function, which can result in a set of ''requests'' for specific active glues and labels on $t$ to transition into specified states. |
| Line 82: | Line 88: | ||
$P_{T ,\tau}$ is defined recursively as follows: | $P_{T ,\tau}$ is defined recursively as follows: | ||
| + | '''Base Set of Assemblies''' $ T \subseteq P_{T ,\tau}$ | ||
| + | |||
| + | '''Combination Transition''' | ||
| − | + | For any 2 active supertiles $A, B \in P_{T ,\tau}$, if $A$ and $B$ are $\tau$ -combinable into active supertile $C$, then $C \in P_{T ,\tau}$ . | |
| − | |||
| − | '''Break Transition''' | + | '''Break Transition''' |
| − | '''Active Glue Transition''' Consider an active supertile $A \in P_{T ,\tau}$ . For each active tile $t \in A$ with $A(x, y) = t = (G, L, \delta, \Pi)$, for all $d \in D$, for all $(g, p) \in G(d)$ and for all $(d, g, q) \in \Pi$, there is a supertile $B \in P_{T ,\tau}$ such that $A$ and $B$ differ only at location $(x, y)$ as follows: $B(x, y) = t$ | + | For any supertile $A \in P_{T ,\tau}$ , if $A$ is $\tau$-breakable into active supertiles $B$ and $C$, then $B, C \in P_{T ,\tau}$ . |
| + | |||
| + | |||
| + | '''Active Glue Transition''' | ||
| + | |||
| + | Consider an active supertile $A \in P_{T ,\tau}$ . For each active tile $t \in A$ with $A(x, y) = t = (G, L, \delta, \Pi)$, for all $d \in D$, for all $(g, p) \in G(d)$ and for all $(d, g, q) \in \Pi$, there is a supertile $B \in P_{T ,\tau}$ such that $A$ and $B$ differ only at location $(x, y)$ as follows: $B(x, y) = t$ | ||
# $\Pi'= \Pi-\{(d, g, q)\}$ and if | # $\Pi'= \Pi-\{(d, g, q)\}$ and if | ||
| Line 98: | Line 111: | ||
(This simply says that any supertile B which can be created from another producible supertile A bysimply executing one of A’s pending actions is also producible.) | (This simply says that any supertile B which can be created from another producible supertile A bysimply executing one of A’s pending actions is also producible.) | ||
| − | '''Active Label Transition''' Active label transitions are defined similar to active glue transitions. | + | '''Active Label Transition''' |
| + | |||
| + | Active label transitions are defined similar to active glue transitions. | ||
| Line 107: | Line 122: | ||
==Example STAM System== | ==Example STAM System== | ||
===Example tile types=== | ===Example tile types=== | ||
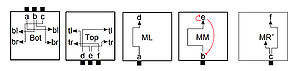
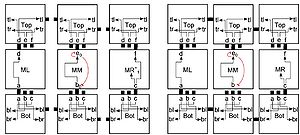
| − | Figure 3 shows a tile set that will be used for the following example. Active tiles are referred by their labels for convenience. The “Bot” tile has four glue actions defined for its transition function, all of which turn | + | Figure 3 shows a tile set that will be used for the following example. Active tiles are referred by their labels for convenience. The “Bot” tile has four glue actions defined for its transition function, all of which turn <tt>on</tt> glues. The “MM” tile includes two glue actions which turn <tt>off</tt> glues: when glue ''e'' on the North binds, both that glue and glue b on the South get $\texttt{off}$ transitions placed into the $\Pi$ multiset of the active tile, which will eventually cause them to be turned <tt>off</tt>. The transition function for the “MR” tile contains a label action, namely when the $c$ glue on the South binds. |
[[File:Example_of_STEM.jpg|thumb|300px|Figure 3. An example active tile set. Credit Asynchronous Signal Passing for Tile Self-Assembly: Fuel Efficient Computation and Efficient Assembly of Shapes]] | [[File:Example_of_STEM.jpg|thumb|300px|Figure 3. An example active tile set. Credit Asynchronous Signal Passing for Tile Self-Assembly: Fuel Efficient Computation and Efficient Assembly of Shapes]] | ||
| Line 116: | Line 131: | ||
===Example STAM transitions=== | ===Example STAM transitions=== | ||
[[File:Producible_supertiles.jpg|thumb|300px|Figure 4(a). Producible supertiles Credit: Asynchronous Signal Passing for Tile Self-Assembly: Fuel Efficient Computation and Efficient Assembly of Shapes]] | [[File:Producible_supertiles.jpg|thumb|300px|Figure 4(a). Producible supertiles Credit: Asynchronous Signal Passing for Tile Self-Assembly: Fuel Efficient Computation and Efficient Assembly of Shapes]] | ||
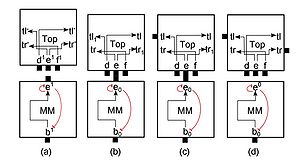
| − | Define an STAM system $(T, 2)$ where $T$ is the tile set shown in Figure 3. Figure 4 shows a set of transitions and producible assemblies within that system. Figure 4(a) shows a “Top” and “MM” tile in their initial configurations (with empty $\Pi$ sets for all active tiles as required, and all superscripts explicitly shown for reference). Figure 4(b) shows the supertile resulting from a combination transition performed on one “Top” and one “MM” tile. Note that the binding of the two $e$ glues causes four glues to have state transitions added to the $\Pi$ multisets the belong to their respective active tile. Figure 4(c) shows the supertile resulting from a glue flip transition performed on the supertile in Figure 4(b), namely the $tl$ glue | + | Define an STAM system $(T, 2)$ where $T$ is the tile set shown in Figure 3. Figure 4 shows a set of transitions and producible assemblies within that system. Figure 4(a) shows a “Top” and “MM” tile in their initial configurations (with empty $\Pi$ sets for all active tiles as required, and all superscripts explicitly shown for reference). Figure 4(b) shows the supertile resulting from a combination transition performed on one “Top” and one “MM” tile. Note that the binding of the two $e$ glues causes four glues to have state transitions added to the $\Pi$ multisets the belong to their respective active tile. Figure 4(c) shows the supertile resulting from a glue flip transition performed on the supertile in Figure 4(b), namely the $tl$ glue <tt>on</tt> the West side of the “Top” tile transitioned to state <tt>on</tt> and that pending transition was removed from the $\Pi$ multiset belonging to its active tile. Figure 4(d) shows the supertile resulting after two glue flip transitions are performed on the supertile in Figure 4(c), namely glue $tr$ <tt>on</tt> the East of “Top” is turned <tt>on</tt> and $e$ on the North of “MM” is turned <tt>off</tt>. |
[[File:Example_transitions_for_the_tile_types.jpg|thumb|300px|Figure 4(b,c). An Example transition for the tile types. Credit: Asynchronous Signal Passing for Tile Self-Assembly: Fuel Efficient Computation and Efficient Assembly of Shapes]] | [[File:Example_transitions_for_the_tile_types.jpg|thumb|300px|Figure 4(b,c). An Example transition for the tile types. Credit: Asynchronous Signal Passing for Tile Self-Assembly: Fuel Efficient Computation and Efficient Assembly of Shapes]] | ||
Latest revision as of 14:57, 26 June 2024
The Signal-passing Tile Assembly Model (STAM)[1] is an asynchronous model of tile self-assembly which is considered as an extension of the 2-Handed Assembly Model (2HAM)[2] and is based on active glues which can dynamically change state, allowing any action of turning a glue on or off, attaching a new tile, or breaking apart an assembly to happen in any order.In STAM basic tiles of the Tile Assembly Model (TAM) are augmented with the ability to receive information, in the form of signals, from neighboring tiles in an assembly, and to pass signals to neighboring tiles. A very important feature of signals is that each signal can only move across any given tile one time - they are not reusable [3].
Generalized model of STAM imposes minimal restrictions on aspects such as the speed of signals and orderings of events. This generalized version, while perhaps difficult to create well-behaved constructions within, provides a framework that is intended to be maximally independent of the specific details of potential physical implementations of actual signal tiles and enriches the tile assembly paradigm with greater capabilities that anticipate advancing techniques in the field of DNA nanotechnology and allow tile assembly to more closely emulate biological and natural processes.[3]
The addition of signaled glue activation and deactivation to tile assembly brings it one step closer to emulating biological processes of self assembly, where communication within a developing and growing living organism are crucial to its survival and success. Communication between tiles and throughout assemblies allows them to take on changing roles in hierarchical assembly processes, resulting in production of organized entities that could continue to function as elements in further tile computation. The generalized model presented here has been designed to take into consideration a DNA implementation of all aspects of signaled assembly: binding, signaling, and glue activation or deactivation.
Contents
Physical Basis for the Model
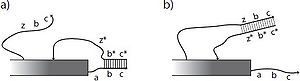
The physical body of a tile might be composed entirely from a DNA origami structure which has more room for signal pathways than smaller DNA structures that have been used to implement the passive tiles of the TAM. Toe-hold mediated DNA strand exchange mechanisms [4][5][6] [7], as shown in Figure 1, provide a basis for a plausible physical implementation of signaling, glue activation and glue deactivation. Signals across individual tiles could potentially be implemented using DNA hybridization cascades such as Hybridization Chain Reaction (HCR) [8], transducers [9], seesaw gates [10], other mechanisms [11], or by DNA walkers. [12][13][14][15]
Letters such as a and \(y\) indicate short sequences of DNA bases and a star indicates the complementary sequence. Rectangles indicate structures, possibly composed of DNA origami, to which the relevant sticky ends of DNA are attached. a) The strand zbc is presumed to be unavailable until freed by a previous signaling cascade (not shown). The sequence labeled \(z\) may then bind at the toehold z8 on the protection strand \(c^{*} b^* z^*\), removing it from the glue strand abc via strand displacement. The protection strand is shown bound only to \(b\) and \(c\), which is enough to prevent interaction with the complementary tile edge shown as long as no toeholds are free to interact. Alternatively, the entire sequence abc could be blocked by the protection strand. b) Once the protection strand is removed, the glue strand abc is active or on.
A glue may be considered 'latent'or 'off' if its DNA sticky end is blocked by being bound to a complementary DNA strand. Activation of a latent glue can be done by the toe-hold mediated removal of a protection strand that blocks a sticky end, (Figure 1). Deactivation can be accomplished by a toehold-mediated mechanism that is essentially the reverse of activation, whereby a protection strand can be released in the vicinity of the glue strand, covering up the sticky end used for binding. By adding more toeholds, one could add a finite number of cycles of activation and deactivation, but each would be mediated by a different activation and deactivation strand, and each effectively consumes DNA fuel. Thus, in the model we have limited activation to occurring only once. More instances of a glue can be
added in a construction if needed.
STAM Notation and Model
High Level Description of the STAM
In the STAM, tiles are allowed to have sets of glues on each edge (as opposed to only one glue per side as in the TAM and 2HAM ). Tiles have an initial state in which each glue is either 'on' or 'latent' (i.e. can be switched on later). Tiles also each implement a transition function which is executed upon the binding of any glue on any edge of that tile. The transition function specifies a set of glues (along with the sides on which those glues are located) and an action for each:
- turn that glue on (only valid if it is currently latent), or
- turn that glue off (valid if it is currently on or latent).
This means that glues can only be on once (although may remain so for an arbitrary amount of time or permanently), either by starting in that state or being switched on from latent, and if they are ever switched to off then no further transitions are allowed for that glue. This essentially provides a single “use” of a glue (and thus the implicit signal sent by its activation and binding). Note that turning a glue off breaks any bond that that glue may have formed with a neighboring tile. The transition function defined for each tile type is allowed a unique set of output actions for the binding event of each glue along its edges. As the STAM is an extension of the 2HAM, binding and breaking can occur between pairs of arbitrarily sized supertiles. In order to allow for physical mechanisms which implement the transition functions of tiles but are arbitrarily slower or faster than the average rates of (super)tile attachments and detachments, rather than immediately enacting the outputs of transition functions, each output action is put into a set of "pending actions" which includes all actions which have not yet been enacted for that glue. An STAM system consists of a set of tiles and a temperature value. To define what is producible from such a system, we use a recursive definition of producible assemblies which starts with the initial tiles and then contains any supertiles which can be formed by doing the following to any producible assembly:
- executing any entry from the pending actions of any one glue within a tile within that supertile (and then that action is removed from the pending set),
- binding with another supertile if they are able for form a \(\tau\)-stable supertile, or
- breaking apart into 2 separate supertiles along a cut whose total strength is less than \(\tau\).
As an overview, tiles in the STAM pass signals to neighboring tiles simply by activating glues which can bind with glues on adjacent edges of neighboring tiles. The information content of a signal is dependent upon the transition function of the receiving tile, that is, by what glue actions the receiving tile initiates upon the binding of its glue. By subsequently activating and deactivating its own glues, the receiving tile can propagate the signal to any of its neighbors. Solely by utilizing the mechanism of glue activation and deactivation initiated and carried out on individual tiles but chained together through series of glue bindings, a global network which is capable of passing information across entire assemblies (and also of allowing them to selectively enable sites for further growth or to discard arbitrary portions of the assembly), is created. However, an important restriction is the fire once nature of the signals, meaning that each glue can only transition to any given state once, and therefore the number of signals which a tile can process is a constant dependent upon the definition of the tile type.
Formal Definition of the Signal Passing Tile Assembly Model
Basic Notation
Let \(D\) denote the set of labels \(\{north, south, east, west\}\), or \(\{N,S,E,W\}\).
Active Glues and Glue States
Let \(\Gamma\) denote a set of \(glue types\). A \(glue\) is an ordered pair \((g,s)\) where \(g \in \Gamma\) is the glue type and \(s \in \mathbb{Z}\) is the glue \(strength\). Note that throughout the remainder of this paper, unless specifically stated, all glues will have strength \(1\) and as shorthand will be denoted simply by their glue types with the strength omitted.
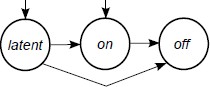
Let \(Q\) = {latent, on, off} be the set of possible \(states\) for a glue. Intuitively, \(\texttt{on}\) is the ``normal, active state of a glue, meaning that it is either able to bind or currently bound. A glue in the \(\texttt{latent}\) state is inactive (and therefore unable to bind), and also has never been \(\texttt{on}\) (or \(\texttt{off}\)). A glue in the \(\texttt{off}\) state is also inactive and unable to bind, but can never be (re)activated. We define an \(active glue\) as an ordered pair \((g,q)\) where \(g \in \Gamma\) is a glue type and \(q \in Q\) is a state.
Active Labels
As in the original TAM, we define a \(label\) as an arbitrary string over some fixed alphabet and labels will be used as non-functional (i.e. they don't participate in tile bindings) means of identifying tile types. Denote as \(\Sigma\) the set of all valid labels. For the self-assembly of patterns (e.g. the weak self-assembly of the Sierpinski triangle), tile labels are the mechanism used for distinguishing between groups of tiles, i.e. those ``in the pattern and those ``outside it. Experimentally, labels can be implemented as DNA loops which protrude above the surfaces of tiles for imaging purposes [15], and thus the motivation exists to allow for the modification of tile labels along with glues. Therefore, we define an \(active label\) is an ordered pair \((x,q)\) where \(x \in \Sigma\) and \(q \in Q\).
Active Tiles and Transition Functions
A generalized active tile type \(t\) is a unit square defined as a \(4\)-tuple \(t = \left(G, L, \delta, \Pi\right)\) where \(G: D \rightarrow P(\Gamma \times Q)\) is a function specifying the set of all active glues present on a given side, \(L\) is the set of all active labels, \(\delta: D \times \Gamma \rightarrow P(((D \times \Gamma \times \{\texttt{on}, \texttt{off}\}) \cup (\Sigma \times \{\texttt{on}, \texttt{off}\}))\) is the transition function and \(\Pi\) is a multiset over \((D \times \Gamma \times \{\texttt{on}, \texttt{off}\}) \cup (\Sigma \times \{\texttt{on}, \texttt{off}\})\). A generalized active tile type \(t = (G, L, \delta, \Pi)\) is an active tile type if, for all \(d \in D\) and for all active glues \((g,q),(g',q') \in G(d)\), \(g \ne g'\). In other words, while a tile side may have multiple glues, there cannot be multiple copies of the same type of glue on a single side.
A transition function \(\delta\) takes as input a direction \(d \in D\) and a glue type \(g \in \Gamma\) (i.e. we say that it is fired by the binding of glue type \(g\) on side \(d\) of \(t\)), and outputs a (possibly empty) set of glue or label actions, i.e., elements of \((D \times \Gamma \times \{\texttt{on}, \texttt{off}\}) \cup (\Sigma \times \{\texttt{on}, \texttt{off}\})\). Consider an active tile type \(t = (G, L, \delta, \Pi)\) and suppose that \((g,q) \in G(d)\) for some \(d \in D\) and \((d', g' ,q') \in \delta(d,g)\). Intuitively, if \(m = \Pi(d', q')\) (i.e., the multiplicity of \((d',q') \in \Pi\)) \(before\) \(\delta\) fires, then \(\Pi(d', q') = m + 1\) after executing \(\delta\). We assume for the sake of convenience that \(\delta\) outputs the empty set for any pair of direction and glue on which \(\delta\) is not explicitly defined. In other words, the binding of a glue on \(t\) fires the transition function, which can result in a set of requests for specific active glues and labels on \(t\) to transition into specified states.
Active Supertiles
Active supertiles in the STAM are defined similarly to supetiles in the 2HAM. Note that only glues which are in the \(\texttt{on}\) state can bind, and only those which are bound contribute to the \(\tau\)-stability of a supertile. When two \(\tau\)-stable supertiles can be translated so that they are non-overlapping and the abutting \(\texttt{on}\) glues can bind to create a cut strength of at least \(\tau\), we say that they are \(\tau\)-\(combinable\). A supertile \(A\) is said to be \(\tau\)-\(breakable\) into supertiles \(B\) and \(C\) if there exists a strength \(\tau' < \tau\) strength cut of the stability graph \(G_A\) that separates the tiles of \(A\) into supertiles \(B\) and \(C\).
Active Supertile Combination
Two active supertiles \(A\) and \(B\) may combine into active supertile \(C\) if the underlying supertiles for \(A\) and \(B\) are \(\tau\)-combinable into the underlying supertile for \(C\). When supertiles combine, all matched glues in the \(\texttt{on}\) state on the boundary between \(A\) and \(B\) are said to bind, and thus fire the transition functions of their respective tiles, causing the necessary states to be added to the pending sets of the targeted tiles.
Active Supertile Breaking
An active supertile \(A\) can break into active supertiles \(B\) and \(C\) if the underlying supertile for \(A\) has a cut of less than \(\tau\)-strength dividing \(A\) into the underlying supertiles for \(B\) and \(C\).
Producible Assemblies
The signal passing tile assembly model is defined in terms of the set of producible active supertiles \(P_{T ,\tau}\) . \(P_{T ,\tau}\) is defined recursively as follows:
Base Set of Assemblies \( T \subseteq P_{T ,\tau}\)
Combination Transition
For any 2 active supertiles \(A, B \in P_{T ,\tau}\), if \(A\) and \(B\) are \(\tau\) -combinable into active supertile \(C\), then \(C \in P_{T ,\tau}\) .
Break Transition
For any supertile \(A \in P_{T ,\tau}\) , if \(A\) is \(\tau\)-breakable into active supertiles \(B\) and \(C\), then \(B, C \in P_{T ,\tau}\) .
Active Glue Transition
Consider an active supertile \(A \in P_{T ,\tau}\) . For each active tile \(t \in A\) with \(A(x, y) = t = (G, L, \delta, \Pi)\), for all \(d \in D\), for all \((g, p) \in G(d)\) and for all \((d, g, q) \in \Pi\), there is a supertile \(B \in P_{T ,\tau}\) such that \(A\) and \(B\) differ only at location \((x, y)\) as follows\[B(x, y) = t\]
- \(\Pi'= \Pi-\{(d, g, q)\}\) and if
- \(p = \texttt{on}\) and \(q = \texttt{off}\) or \(p = \texttt{latent}\) and \(q = \texttt{off}\) or \(p = \texttt{latent}\) and \(q = \texttt{on}\), then for all \(d\neq d\)
(This simply says that any supertile B which can be created from another producible supertile \(A\) by simply executing one of A’s pending actions is also producible.)
Active Label Transition Active label transitions are defined similar to active glue transitions. (This simply says that any supertile B which can be created from another producible supertile A bysimply executing one of A’s pending actions is also producible.)
Active Label Transition
Active label transitions are defined similar to active glue transitions.
Terminal Assemblies
The set of producible assemblies of an STAM system defines the collection of active supertiles that can occur throughout the assembly process. The terminal set of assemblies \(A_{\square}[T, \tau ]\) of an STAM system (T, \(\tau\) ) defines the subset of producible assemblies for which no combination, break, glue transition, or label transition is possible. Conceptually, the terminal assembly set represents the sink state of the assembly system in which the system has been given enough time for all assemblies to reach a terminal state. The terminal set of assemblies is considered the output of an STAM system.
Example STAM System
Example tile types
Figure 3 shows a tile set that will be used for the following example. Active tiles are referred by their labels for convenience. The “Bot” tile has four glue actions defined for its transition function, all of which turn on glues. The “MM” tile includes two glue actions which turn off glues: when glue e on the North binds, both that glue and glue b on the South get \(\texttt{off}\) transitions placed into the \(\Pi\) multiset of the active tile, which will eventually cause them to be turned off. The transition function for the “MR” tile contains a label action, namely when the \(c\) glue on the South binds.
Example STAM transitions
Define an STAM system \((T, 2)\) where \(T\) is the tile set shown in Figure 3. Figure 4 shows a set of transitions and producible assemblies within that system. Figure 4(a) shows a “Top” and “MM” tile in their initial configurations (with empty \(\Pi\) sets for all active tiles as required, and all superscripts explicitly shown for reference). Figure 4(b) shows the supertile resulting from a combination transition performed on one “Top” and one “MM” tile. Note that the binding of the two \(e\) glues causes four glues to have state transitions added to the \(\Pi\) multisets the belong to their respective active tile. Figure 4(c) shows the supertile resulting from a glue flip transition performed on the supertile in Figure 4(b), namely the \(tl\) glue on the West side of the “Top” tile transitioned to state on and that pending transition was removed from the \(\Pi\) multiset belonging to its active tile. Figure 4(d) shows the supertile resulting after two glue flip transitions are performed on the supertile in Figure 4(c), namely glue \(tr\) on the East of “Top” is turned on and \(e\) on the North of “MM” is turned off.
References
- ↑
Jennifer E. Padilla, Matthew J. Patitz, Raul Pena, Robert T. Schwellery, Nadrian C. Seeman, Robert Sheline, Scott M. Summers,, Xingsi Zhong - Asynchronous Signal Passing for Tile Self-Assembly: Fuel Efficient Computation and Efficient Assembly of Shapes
- Unconventional Computation and Natural Computation Lecture Notes in Computer Science 7956:174-185,2013
- BibtexAuthor : Jennifer E. Padilla, Matthew J. Patitz, Raul Pena, Robert T. Schwellery, Nadrian C. Seeman, Robert Sheline, Scott M. Summers,, Xingsi Zhong
Title : Asynchronous Signal Passing for Tile Self-Assembly: Fuel Efficient Computation and Efficient Assembly of Shapes
In : Unconventional Computation and Natural Computation Lecture Notes in Computer Science -
Address :
Date : 2013
- ↑
Qi Cheng, Gagan Aggarwal, Michael H. Goldwasser, Ming-Yang Kao, Robert T. Schweller, Pablo Moisset de Espanés - Complexities for Generalized Models of Self-Assembly
- ↑ 3.0 3.1
J.E. Padilla, W. Liu,, N.C. Seeman - Hierarchical self assembly of patterns from the Robinson tilings: DNA tile design in an enhanced tile assembly model
- ↑
G. Seelig, D. Soloveichik, D.Y. Zhang,, E. Winfree - Enzyme-free Nucleic Acid Logic Circuits
- ↑
P. Yin, H.M.T. Choi, C.R. Calvert,, N.A. Pierce - Programming biomolecular self-assembly pathways
- ↑
B. Yurke, A.J. Turberfield, A.P. Mills, F.C. Simmel,, J.L. Neumann - A DNA-fuelled molecular machine made of DNA
- ↑
D.Y. Zhang, G. Seelig - Dynamic DNA nanotechnology using strand-displacement reactions
- ↑
R.M. Dirks, N.A. Pierce - Triggered amplification by hybridization chain reaction
- Proceedings of the National Academy of Sciences of the United States of America 101(43):15275–15278,2004
- BibtexAuthor : R.M. Dirks, N.A. Pierce
Title : Triggered amplification by hybridization chain reaction
In : Proceedings of the National Academy of Sciences of the United States of America -
Address :
Date : 2004
- ↑
G. Seelig, D. Soloveichik, D.Y. Zhang,, E. Winfree - Enzyme-free nucleic acid logic circuits
- ↑
L. Qian, E. Winfree - A simple DNA gate motif for synthesizing large-scale circuits
- ↑
P. Yin, H.M.T. Choi, C.R. Calvert,, N.A. Pierce - Programming biomolecular self-assembly pathways
- ↑
K. Lund, A.J. Manzo, N. Dabby, N. Michelotti, A. Johnson-Buck, J. Nangreave, S. Taylor, R. Pei, M.N. Stojanovic,, N.G. Walter - Molecular robots guided by prescriptive landscapes
- ↑
T. Omabegho, R. Sha,, N.C. Seeman - A bipedal DNA brownian motor with coordinated legs
- ↑
S.F.J. Wickham, M. Endo, Y. Katsuda, K. Hidaka, J. Bath, H. Sugiyama,, A.J. Turberfield - Direct observation of stepwise movement of a synthetic molecular transporter
- ↑ 15.0 15.1
F. Liu, R. Sha,, N.C. Seeman - Modifying the surface features of two-dimensional DNA crystals
- Journal of the American Chemical Society 121(5):917-922,1999
- BibtexAuthor : F. Liu, R. Sha,, N.C. Seeman
Title : Modifying the surface features of two-dimensional DNA crystals
In : Journal of the American Chemical Society -
Address :
Date : 1999