Difference between revisions of "Sierpinski triangle in the kTAM"
m (Added this page to relevant category.) |
|||
| (10 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | [[Category:Self-assembly]] | ||
| + | |||
==Introduction== | ==Introduction== | ||
| − | The kinetic tile assembly model (kTAM) builds upon the abstract model (aTAM) by allowing not only for the binding of tiles, but also for the unbinding of tiles. At a high level you might think about the binding and unbinding in the kTAM as growth and decay, or more formally as association and dissociation. Further, the kTAM also allows for tiles to bind which have no matching glues. The binding allowances introduced in the kTAM are there to mimic the chemical behavior of DNA. | + | The [[Kinetic Tile Assembly Model (kTAM) | kinetic tile assembly model (kTAM)]] builds upon the [[Abstract Tile Assembly Model (aTAM) | abstract model (aTAM)]] by allowing not only for the binding of tiles, but also for the unbinding of tiles. At a high level you might think about the binding and unbinding in the kTAM as growth and decay, or more formally as association and dissociation. Further, the kTAM also allows for tiles to bind which have no matching glues. The binding allowances introduced in the kTAM are there to mimic the chemical behavior of DNA. |
This tutorial will step you through the basic concepts of the kTAM. While working with the kTAM you will notice that there are trade-offs between speed of assembly and accuracy of assembly. For example, it is possible to have an assembly that builds very quickly to a given size, yet without proper tile types, the assembly will be filled with errors. The other undesirable alternative is to build very slowly but accurately. Fortunately, there is a middle path that we can take known broadly as error management. Error management within the kTAM involves recognizing the potential errors that can occur for a tile set and then redesigning that tile set so that it is more resilient to errors, still produces the expected output, and does so in a shorter period of time. | This tutorial will step you through the basic concepts of the kTAM. While working with the kTAM you will notice that there are trade-offs between speed of assembly and accuracy of assembly. For example, it is possible to have an assembly that builds very quickly to a given size, yet without proper tile types, the assembly will be filled with errors. The other undesirable alternative is to build very slowly but accurately. Fortunately, there is a middle path that we can take known broadly as error management. Error management within the kTAM involves recognizing the potential errors that can occur for a tile set and then redesigning that tile set so that it is more resilient to errors, still produces the expected output, and does so in a shorter period of time. | ||
| − | + | ===kTAM in TAS=== | |
| + | The previous tutorials have only been concerned with implementing tile assemblies in the aTAM simulation mode. Now, however, we need to change simulation modes to kTAM. To do this find the Simulation Window and under the menu bar go to: ''Option -> Set simulation mode -> kTAM''. | ||
| + | The configuration window will appear on the left side of the Simulation Space. Within this window you can dynamically change the disassociation rate ('''G<sub>se</sub>''') and the association rate ('''G<sub>mc</sub>'''). By default '''G<sub>se</sub>''' is set to 10.00 and '''G<sub>mc</sub>''' is set to 19.80. | ||
| − | == | + | ====Preferred Performance Settings==== |
| − | + | While experimenting with the kTAM using TAS we recommend changing the following settings: | |
| − | # | + | # Adjust the refresh rate of the assembly to between 1,000 and 10,000. To do this go to the Simulation Window then:<br />''Appearance -> Refresh every -> Custom rate... -> A pop up box will appear where you may change the refresh rate'' |
| − | + | # Turning off caching, or the saving of past tile placements. To do this go to the Simulation Window then:<br />''Control -> Disable cache mode'' | |
| − | |||
| − | ===Growth Errors=== | + | ==[[Kinetic_Tile_Assembly_Model_(kTAM)#Error_Types | Error types]]== |
| − | A growth error occurs when a tile binds to a frontier-tile but the adjacent glues of the respective binding edges do not match. The disassociation rate | + | There are three basic error types that can occur during assembly in the kTAM: |
| + | #[[ Growth Errors | Growth (or Mismatch)]] | ||
| + | #[[ Facet Errors | Facet]] | ||
| + | #[[Nucleation Errors | Nucleation]] | ||
| + | |||
| + | ===[[Growth Errors]]=== | ||
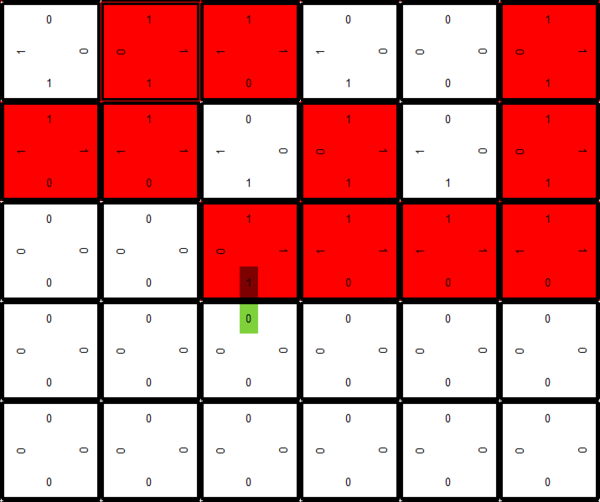
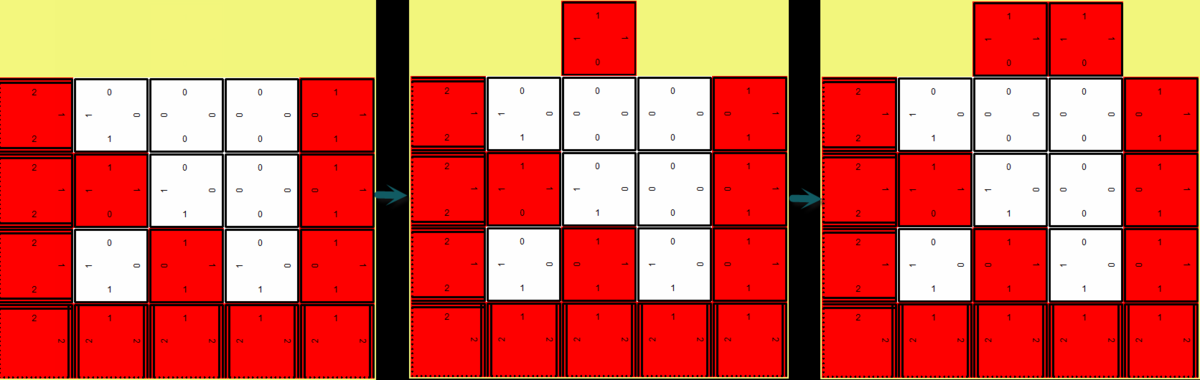
| + | A growth error occurs when a tile binds to a frontier-tile but the adjacent glues of the respective binding edges do not match. The disassociation rate '''G<sub>se</sub>''' within the kTAM dictates how long this mismatched edge will stay bound. The higher the '''G<sub>se</sub>''' the longer the error can persist before unbinding. However, even with a normal ratio of '''G<sub>mc</sub>/G<sub>se</sub>''' it is still possible that the mismatched tiles will stay bound long enough for appropriately matched tiles to fill out the space around the error and permanently bind it into place. Once the anomaly is bound in place further deviations from the desired assembly shape may be propagated throughout the assembly. A visual example of this can be seen below in a 7-tile Sierpinski assembly. The top image is a zoomed in section of the assembly that shows the glue labels of each tile. Notice that under the green highlight there is a matching error between the respective tile edges. The same assembly is shown in the second image but zoomed out. The green mark represents the only binding error in the entire assembly, but as can be seen, it ruined the expected periodicity of the assembly. | ||
[[File:KTAM_growth_error_7_tiles.png|thumb|center|upright=2.0|alt=Growth Error|Growth error.]] | [[File:KTAM_growth_error_7_tiles.png|thumb|center|upright=2.0|alt=Growth Error|Growth error.]] | ||
| Line 20: | Line 29: | ||
[[File:KTAM_growth_error_7_tiles_zoomout.png|thumb|center|upright=2.0|alt=Growth Error|Growth error, zoomed out.]] | [[File:KTAM_growth_error_7_tiles_zoomout.png|thumb|center|upright=2.0|alt=Growth Error|Growth error, zoomed out.]] | ||
| − | ===Facet Errors=== | + | ===[[Facet Errors]]=== |
| − | Facet errors, like growth errors, occur along the frontier of the assembly and between two tile edges which have insufficient strength to form a permanent attachment given the current | + | Facet errors, like growth errors, occur along the frontier of the assembly and between two tile edges which have insufficient strength to form a permanent attachment given the current '''G<sub>mc</sub>/G<sub>se</sub>'''. Facet errors become permanent when they are locked into place by subsequent tile addition. Unlike growth errors, however, facet errors are characterized by matching edges. |
[[File:KTAM_facet_error_demo.png|thumb|center|upright=4.0|alt=Facet Error]] | [[File:KTAM_facet_error_demo.png|thumb|center|upright=4.0|alt=Facet Error]] | ||
| − | ===Nucleation Errors=== | + | ===[[Nucleation Errors]]=== |
| − | A nucleation error occurs when tiles associate with each other outside of the seed structure and start another seeded structure. | + | A nucleation error occurs when tiles associate with each other outside of the seed structure and start another seeded structure. |
==Error Management within the kTAM== | ==Error Management within the kTAM== | ||
===Growth Errors=== | ===Growth Errors=== | ||
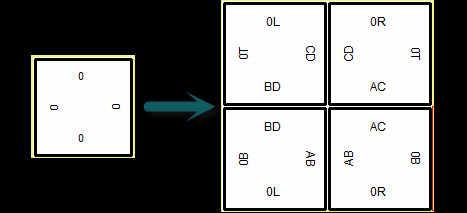
| − | A common technique to reduce growth errors is called proofreading. With the proofreading method individual tile types are replaced by ''n'' X ''n'' blocks of unique tile types. The perimeter of the ''n'' X ''n'' block formed represents the same glues as the original tile, only the original glues are now split into ''n'' separate glues. For example, imagine you are going to implement a proofreading scheme where each tile in your original set is going to be replaced by a ''2'' X ''2'' block of tiles. This conversion might look like the following: | + | A common technique to reduce growth errors, introduced in <ref name=WinBek03 />, is called [[Error Suppresion Via Block Replacement | proofreading]]. With the proofreading method individual tile types are replaced by ''n'' X ''n'' blocks of unique tile types. The perimeter of the ''n'' X ''n'' block formed represents the same glues as the original tile, only the original glues are now split into ''n'' separate glues. For example, imagine you are going to implement a proofreading scheme where each tile in your original set is going to be replaced by a ''2'' X ''2'' block of tiles. This conversion might look like the following: |
[[File:Proofreading_example_0.png|thumb|center|upright=4.0|alt=Facet Error]] | [[File:Proofreading_example_0.png|thumb|center|upright=4.0|alt=Facet Error]] | ||
| − | The interior glues for each expanded tile will be unique to that group | + | The interior glues (AB, AC, BD, CD) for each expanded tile will be unique to that group. The exterior glues (0L, 0R, 0T, 0B) can be shared by more than one tile type. to the so that this transformed tile can still interact appropriately with the other tiles in the tile-set. |
| − | The goal of proofreading is to force multiple errors to occur before a ''n'' X ''n'' block can fully form, this consequently results in fewer errors being locked in. | + | The goal of proofreading is to force multiple errors to occur before a ''n'' X ''n'' block can fully form, this consequently results in fewer errors being locked in. |
===Exercise=== | ===Exercise=== | ||
| Line 47: | Line 56: | ||
[[File:KTAM_proofreading_2x2.png|thumb|center|upright=2.0|alt=Proofreading2x2]] | [[File:KTAM_proofreading_2x2.png|thumb|center|upright=2.0|alt=Proofreading2x2]] | ||
| + | |||
| + | ==References== | ||
| + | <references> | ||
| + | |||
| + | <ref name =WinBek03><bibtex> | ||
| + | @inproceedings{WinBek03, | ||
| + | title = {Proofreading Tile Sets: Error Correction for Algorithmic Self-Assembly}, | ||
| + | author = {Erik Winfree and Renat Bekbolatov}, | ||
| + | booktitle = {DNA}, | ||
| + | editor = {Junghuei Chen and John H. Reif}, | ||
| + | pages = {126-144}, | ||
| + | publisher = {Springer}, | ||
| + | series = {Lecture Notes in Computer Science}, | ||
| + | url = {http://dblp.uni-trier.de/db/conf/dna/dna2003.html#WinfreeB03}, | ||
| + | volume = {2943}, | ||
| + | year = {2003}, | ||
| + | biburl = {http://www.bibsonomy.org/bibtex/2039454b0f808ce60fd853f6e7d9d4b2a/dblp}, | ||
| + | description = {dblp}, | ||
| + | ee = {http://springerlink.metapress.com/openurl.asp?genre=article&issn=0302-9743&volume=2943&spage=126}, isbn = {3-540-20930-1}, date = {2004-02-02}, | ||
| + | keywords = {dblp } | ||
| + | } | ||
| + | </bibtex></ref> | ||
| + | |||
| + | </references> | ||
Latest revision as of 13:53, 11 June 2019
Contents
Introduction
The kinetic tile assembly model (kTAM) builds upon the abstract model (aTAM) by allowing not only for the binding of tiles, but also for the unbinding of tiles. At a high level you might think about the binding and unbinding in the kTAM as growth and decay, or more formally as association and dissociation. Further, the kTAM also allows for tiles to bind which have no matching glues. The binding allowances introduced in the kTAM are there to mimic the chemical behavior of DNA.
This tutorial will step you through the basic concepts of the kTAM. While working with the kTAM you will notice that there are trade-offs between speed of assembly and accuracy of assembly. For example, it is possible to have an assembly that builds very quickly to a given size, yet without proper tile types, the assembly will be filled with errors. The other undesirable alternative is to build very slowly but accurately. Fortunately, there is a middle path that we can take known broadly as error management. Error management within the kTAM involves recognizing the potential errors that can occur for a tile set and then redesigning that tile set so that it is more resilient to errors, still produces the expected output, and does so in a shorter period of time.
kTAM in TAS
The previous tutorials have only been concerned with implementing tile assemblies in the aTAM simulation mode. Now, however, we need to change simulation modes to kTAM. To do this find the Simulation Window and under the menu bar go to: Option -> Set simulation mode -> kTAM. The configuration window will appear on the left side of the Simulation Space. Within this window you can dynamically change the disassociation rate (Gse) and the association rate (Gmc). By default Gse is set to 10.00 and Gmc is set to 19.80.
Preferred Performance Settings
While experimenting with the kTAM using TAS we recommend changing the following settings:
- Adjust the refresh rate of the assembly to between 1,000 and 10,000. To do this go to the Simulation Window then:
Appearance -> Refresh every -> Custom rate... -> A pop up box will appear where you may change the refresh rate - Turning off caching, or the saving of past tile placements. To do this go to the Simulation Window then:
Control -> Disable cache mode
Error types
There are three basic error types that can occur during assembly in the kTAM:
Growth Errors
A growth error occurs when a tile binds to a frontier-tile but the adjacent glues of the respective binding edges do not match. The disassociation rate Gse within the kTAM dictates how long this mismatched edge will stay bound. The higher the Gse the longer the error can persist before unbinding. However, even with a normal ratio of Gmc/Gse it is still possible that the mismatched tiles will stay bound long enough for appropriately matched tiles to fill out the space around the error and permanently bind it into place. Once the anomaly is bound in place further deviations from the desired assembly shape may be propagated throughout the assembly. A visual example of this can be seen below in a 7-tile Sierpinski assembly. The top image is a zoomed in section of the assembly that shows the glue labels of each tile. Notice that under the green highlight there is a matching error between the respective tile edges. The same assembly is shown in the second image but zoomed out. The green mark represents the only binding error in the entire assembly, but as can be seen, it ruined the expected periodicity of the assembly.
Facet Errors
Facet errors, like growth errors, occur along the frontier of the assembly and between two tile edges which have insufficient strength to form a permanent attachment given the current Gmc/Gse. Facet errors become permanent when they are locked into place by subsequent tile addition. Unlike growth errors, however, facet errors are characterized by matching edges.
Nucleation Errors
A nucleation error occurs when tiles associate with each other outside of the seed structure and start another seeded structure.
Error Management within the kTAM
Growth Errors
A common technique to reduce growth errors, introduced in [1], is called proofreading. With the proofreading method individual tile types are replaced by n X n blocks of unique tile types. The perimeter of the n X n block formed represents the same glues as the original tile, only the original glues are now split into n separate glues. For example, imagine you are going to implement a proofreading scheme where each tile in your original set is going to be replaced by a 2 X 2 block of tiles. This conversion might look like the following:
The interior glues (AB, AC, BD, CD) for each expanded tile will be unique to that group. The exterior glues (0L, 0R, 0T, 0B) can be shared by more than one tile type. to the so that this transformed tile can still interact appropriately with the other tiles in the tile-set.
The goal of proofreading is to force multiple errors to occur before a n X n block can fully form, this consequently results in fewer errors being locked in.
Exercise
As an exercise for using the kTAM with TAS implement the 7-tile Sierpinski Triangle developed in prior tutorials with proofreading such that:
- Four of the tiles are replaced by a 2 X 2 set
- Two of the tiles are replaced by a 1 X 2 set
- One tile remains the same
In total your new tile set should have 21 unique tiles and the assembly should look similar to the below picture.
References
- ↑
Erik Winfree, Renat Bekbolatov - Proofreading Tile Sets: Error Correction for Algorithmic Self-Assembly