Difference between revisions of "Abstract Tile Assembly Model (aTAM)"

From self-assembly wiki
Jump to navigation Jump to search
(Created page with "The aTAM was developed to, in some sense, be an effectivization of Wang tiling. (See Wang_Tiling for more about this relationship.) Namely, it provides a defined process by...")
 
(→‎Formal Definition of the Model)
 
(37 intermediate revisions by 4 users not shown)
Line 1: Line 1:
−
The aTAM was developed to, in some sense, be an effectivization of Wang tiling.  (See [[Wang_Tiling]] for more about this relationship.)  Namely, it provides a defined process by which an initial (called the \emph{seed}) assembly can grow into a resultant structure.  This is essentially accomplished by assigning a positive integer \emph{strength} value to each edge color in a set of Wang tiles and stipulating that when two tile edges are adjacent, if their colors match then the edges bind with force equivalent to the strength of the edge color.  Then, starting with a preformed seed assembly (usually taken to be a single tile of a specified type), additional tiles can attach one at a time as long as the sum of the strengths of the bonds that each makes with tiles already in the assembly meets a system wide threshold value called the \emph{temperature}.
+
__TOC__
 +
==Informal Description of the Model==
 +
The aTAM was developed to, in some sense, be an effectivization of Wang tiling.  (See [[Wang Tiling]] for more about this relationship.)  Namely, it provides a defined process by which an initial (called the seed) assembly can grow into a resultant structure.  This is essentially accomplished by assigning a positive integer strength value to each edge color in a set of Wang tiles and stipulating that when two tile edges are adjacent, if their colors match then the edges bind with force equivalent to the strength of the edge color.  Then, starting with a preformed seed assembly (usually taken to be a single tile of a specified type), additional tiles can attach one at a time as long as the sum of the strengths of the bonds that each makes with tiles already in the assembly meets a system wide threshold value called the [[Temperature | temperature]].
  
 +
==Formal Definition of the Model==
 +
$\newcommand{\res}[1]{\textrm{res}(#1)}$
 +
$\newcommand{\termasm}[1]{\mathcal{A}_{\Box}[\mathcal{#1}]}
 +
\newcommand{\prodasm}[1]{\mathcal{A}[\mathcal{#1}]}$
 
We now give a brief formal definition of the aTAM. See <ref name=Winf98 /> <ref name=RotWin00 /> <ref name=Roth01 /> <ref name=jSSADST /> for other developments of the model.  Our notation is that of <ref name=jSSADST />, which also contains a more complete definition.
 
We now give a brief formal definition of the aTAM. See <ref name=Winf98 /> <ref name=RotWin00 /> <ref name=Roth01 /> <ref name=jSSADST /> for other developments of the model.  Our notation is that of <ref name=jSSADST />, which also contains a more complete definition.
  
−
Given a set $T$ of tile types, an {\it assembly} is a partial function $\pfunc{\alpha}{\mathbb{Z}^2}{T}$. An assembly is {\it $\tau$-stable}
+
Given a set $T$ of tile types, an [[Assembly | assembly]] is a partial function ${\alpha}:{\mathbb{Z}^2} \dashrightarrow {T}$. An assembly is [[Assembly#Tau-stable Assembly| $\tau$-stable]] if it cannot be broken up into smaller assemblies without breaking bonds of total strength at least $\tau$, for some $\tau \in \mathbb{N}$.
−
if it cannot be broken up into smaller assemblies without breaking bonds of total strength at least $\tau$, for some $\tau \in \mathbb{N}$.
 
  
−
Self-assembly begins with a {\it seed assembly} $\sigma$ and
+
Self-assembly begins with a [[Assembly#Seed Assembly| seed assembly]] $\sigma$ and
 
proceeds asynchronously and nondeterministically, with tiles
 
proceeds asynchronously and nondeterministically, with tiles
 
adsorbing one at a time to the existing assembly in any manner that
 
adsorbing one at a time to the existing assembly in any manner that
−
preserves $\tau$-stability at all times.  A {\it tile assembly system}
+
preserves $\tau$-stability at all times.  A [[Tile Assembly System (TAS)#Abstract Tile Assembly Model Tile Assembly System (aTAM TAS) | tile assembly system (TAS)]] is an ordered triple $\mathcal{T} = (T, \sigma, \tau)$,
−
({\it TAS}) is an ordered triple $\mathcal{T} = (T, \sigma, \tau)$,
 
 
where $T$ is a finite set of tile types, $\sigma$ is a seed assembly
 
where $T$ is a finite set of tile types, $\sigma$ is a seed assembly
−
with finite domain, and $\tau \in \N$.  A {\it generalized tile
+
with finite domain, and $\tau \in \mathbb{N}$.  A [[Tile Assembly System (TAS)#Abstract Tile Assembly Model Generalized Tile Assembly System (aTAM GTAS) | generalized tile assembly system (GTAS)]]
−
assembly system} ({\it GTAS})
 
 
is defined similarly, but without the finiteness requirements.  We
 
is defined similarly, but without the finiteness requirements.  We
−
write $\prodasm{\mathcal{T}}$ for the set of all assemblies that can arise
+
write $\mathcal{A}[\mathcal{T}]$ for the set of all assemblies that can arise
 
(in finitely many steps or in the limit) from $\mathcal{T}$.  An
 
(in finitely many steps or in the limit) from $\mathcal{T}$.  An
−
assembly $\alpha \in \prodasm{\mathcal{T}}$ is {\it terminal}, and we write $\alpha \in
+
assembly $\alpha \in \mathcal{A}[\mathcal{T}]$ is [[Assembly#Terminal Assembly| terminal]], and we write $\alpha \in
−
\termasm{\mathcal{T}}$, if no tile can be $\tau$-stably added to it. It is clear that $\termasm{\mathcal{T}} \subseteq \prodasm{\mathcal{T}}$.
+
\mathcal{A}_{\Box}[\mathcal{T}]$, if no tile can be $\tau$-stably added to it. It is clear that $\mathcal{A}_{\Box}[\mathcal{T}] \subset \mathcal{A}[\mathcal{T}]$.
  
−
An assembly sequence in a TAS $\mathcal{T}$ is a (finite or infinite) sequence $\vec{\alpha} = (\alpha_0,\alpha_1,\ldots)$ of assemblies in which each $\alpha_{i+1}$ is obtained from $\alpha_i$ by the addition of a single tile. The \emph{result} $\res{\vec{\alpha}}$ of such an assembly sequence is its unique limiting assembly. (This is the last assembly in the sequence if the sequence is finite.) The set $\prodasm{T}$ is partially ordered by the relation $\longrightarrow$ defined by
+
An assembly [[Assembly#Assembly Sequence| sequence]] in a TAS $\mathcal{T}$ is a (finite or infinite) sequence $\vec{\alpha} = (\alpha_0,\alpha_1,\ldots)$ of assemblies in which each $\alpha_{i+1}$ is obtained from $\alpha_i$ by the addition of a single tile. The [[Assembly#Assembly Sequence| result]] $\res{\vec{\alpha}}$ of such an assembly sequence is its unique limiting assembly. (This is the last assembly in the sequence if the sequence is finite.) The set $\mathcal{A}[\mathcal{T}]$ is partially ordered by the relation $\longrightarrow$ defined by
 +
 
 +
$$
 
\begin{eqnarray*}
 
\begin{eqnarray*}
−
\alpha \longrightarrow \alpha' & \textmd{iff} & \textmd{there is an assembly sequence } \vec{\alpha} = (\alpha_0,\alpha_1,\ldots) \\
+
\alpha \longrightarrow \alpha' & \textrm{iff} & \textrm{there is an assembly sequence } \vec{\alpha} = (\alpha_0,\alpha_1,\ldots) \\&              & \textrm{such that } \alpha_0 = \alpha \textrm{ and } \alpha' = \res{\vec{\alpha}}.\\  
−
                              &              & \textmd{such that } \alpha_0 = \alpha \textmd{ and } \alpha' = \res{\vec{\alpha}}. \\
 
 
\end{eqnarray*}
 
\end{eqnarray*}
 +
$$
  
−
We say that $\mathcal{T}$ is \emph{directed} (a.k.a. \emph{deterministic}, \emph{confluent}, \emph{produces a unique assembly}) if the relation $\longrightarrow$ is directed, i.e., if for all $\alpha,\alpha' \in \prodasm{T}$, there exists $\alpha'' \in \prodasm{T}$ such that $\alpha \longrightarrow \alpha''$ and $\alpha' \longrightarrow \alpha''$. It is easy to show that $\mathcal{T}$ is directed if and only if there is a unique terminal assembly $\alpha \in \prodasm{T}$ such that $\sigma \longrightarrow \alpha$.
+
We say that $\mathcal{T}$ is [[Directed Tile Assembly Systems | directed]] if the relation $\longrightarrow$ is directed, i.e., if for all $\alpha,\alpha' \in \prodasm{T}$, there exists $\alpha'' \in \prodasm{T}$ such that $\alpha \longrightarrow \alpha''$ and $\alpha' \longrightarrow \alpha''$. It is easy to show that $\mathcal{T}$ is directed if and only if there is a unique terminal assembly $\alpha \in \mathcal{A}[\mathcal{T}]$ such that $\sigma \longrightarrow \alpha$.
  
 
In general, even a directed TAS may have a very large
 
In general, even a directed TAS may have a very large
Line 33: Line 38:
 
very difficult to prove that a TAS is directed.  Fortunately,
 
very difficult to prove that a TAS is directed.  Fortunately,
 
Soloveichik and Winfree <ref name=SolWin07 /> have defined a
 
Soloveichik and Winfree <ref name=SolWin07 /> have defined a
−
property, {\it local determinism}, of assembly sequences and proven
+
property, [[Directed Tile Assembly Systems#Local Determinism | local determinism]], of assembly sequences and proven
−
the remarkable fact that, if a TAS $\mathcal{T}$ has {\it any}
+
the remarkable fact that, if a TAS $\mathcal{T}$ has ''any''
 
assembly sequence that is locally deterministic, then $\mathcal{T}$
 
assembly sequence that is locally deterministic, then $\mathcal{T}$
 
is directed. Intuitively, an assembly sequence $\vec{\alpha}$ is locally deterministic if (1) each
 
is directed. Intuitively, an assembly sequence $\vec{\alpha}$ is locally deterministic if (1) each
−
tile added in $\vec{\alpha}$ ``just barely'' binds to the existing assembly (meaning that is does so with a summed strength of bonds equal to exactly $\tau$);
+
tile added in $\vec{\alpha}$ "just barely" binds to the existing assembly (meaning that is does so with a summed strength of bonds equal to exactly $\tau$);
 
(2) if a tile of type $t_0$ at a location $\vec{m}$ and its
 
(2) if a tile of type $t_0$ at a location $\vec{m}$ and its
−
immediate ``output-neighbors'' (i.e. those adjacent tiles which bound after the tile at $\vec{m}$) are deleted from the {\it result} of
+
immediate "output-neighbors" (i.e. those adjacent tiles which bound after the tile at $\vec{m}$) are deleted from the [[Assembly#Assembly Sequence | result]] of
 
$\vec{\alpha}$, then no tile of type $t \ne t_0$ can attach itself
 
$\vec{\alpha}$, then no tile of type $t \ne t_0$ can attach itself
 
to the thus-obtained configuration at location $\vec{m}$; and (3)
 
to the thus-obtained configuration at location $\vec{m}$; and (3)
Line 45: Line 50:
  
  
−
A set $X \subseteq \Z^2$ {\it weakly self-assembles} if there exists
+
A set $X \in \mathbb{Z}^2$ [[Weak Self-Assembly | weakly self-assembles]] if there exists
 
a TAS ${\mathcal T} = (T, \sigma, \tau)$ and a set $B \subseteq T$
 
a TAS ${\mathcal T} = (T, \sigma, \tau)$ and a set $B \subseteq T$
 
such that $\alpha^{-1}(B) = X$ holds for every terminal assembly
 
such that $\alpha^{-1}(B) = X$ holds for every terminal assembly
 
$\alpha \in \termasm{T}$.  Essentially, weak self-assembly can be thought of
 
$\alpha \in \termasm{T}$.  Essentially, weak self-assembly can be thought of
−
as the creation (or ``painting'') of a pattern of tiles from $B$ (usually taken to be a
+
as the creation (or "painting") of a pattern of tiles from $B$ (usually taken to be a
−
unique ``color'') on a possibly larger ``canvas'' of un-colored tiles.
+
unique "color") on a possibly larger "canvas" of un-colored tiles.
  
−
A set $X$ \emph{strictly self-assembles} if there is a TAS $\mathcal{T}$ for
+
A set $X$ [[Strict Self-Assembly | strictly self-assembles]] if there is a TAS $\mathcal{T}$ for
−
which every assembly $\alpha\in\termasm{T}$ satisfies $\dom \alpha =
+
which every assembly $\alpha \in \mathcal{A}_{\Box}[\mathcal{T}]$ satisfies $\dom \alpha =
 
X$. Essentially, strict self-assembly means that tiles are only placed
 
X$. Essentially, strict self-assembly means that tiles are only placed
 
in positions defined by the shape.  Note that if $X$ strictly self-assembles, then $X$ weakly
 
in positions defined by the shape.  Note that if $X$ strictly self-assembles, then $X$ weakly
 
self-assembles. (Let all tiles be in $B$.)
 
self-assembles. (Let all tiles be in $B$.)
−
 
+
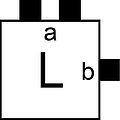
[[File:Example-tile.jpg|thumb|right|120px|An example tile that has glue of strength 0 on the left (W) and bottom (S), glue of color 'a' and strength 2 on the top (N), and glue of color 'b' and strength 1 on the right (E). This tile also has label 'L'..]]
 
Tiles are often depicted as squares whose various sides contain 0, 1, or 2 attached black squares,
 
Tiles are often depicted as squares whose various sides contain 0, 1, or 2 attached black squares,
 
indicating whether the glue strengths on
 
indicating whether the glue strengths on
 
these sides are 0, 1, or 2, respectively. Thus, for example, a tile
 
these sides are 0, 1, or 2, respectively. Thus, for example, a tile
−
of the type shown in Figure~\ref{fig:exampletile}
+
of the type shown to the right has glue of strength 0 on the left (W) and bottom (S), glue of color 'a' and strength 2 on the top (N), and glue of color 'b' and strength 1 on the
−
\begin{figure}[htp]
 
−
\begin{center}
 
−
\includegraphics[width=0.54in]{eps-images/example-tile.eps}
 
−
\caption{An example tile type.}
 
−
\label{fig:exampletile}
 
−
\end{center}
 
−
\end{figure}
 
−
has glue of strength 0 on the left (W) and bottom (S), glue of color `a' and
 
−
strength 2 on the top (N), and glue of color `b' and strength 1 on the
 
 
right (E). This tile also has a label `L', which plays no formal role
 
right (E). This tile also has a label `L', which plays no formal role
 
but may aid our understanding and discussion of the construction.
 
but may aid our understanding and discussion of the construction.
 +
<br>
 +
<br>
 +
<br>
 +
 +
==Example: A Binary Counter==
 +
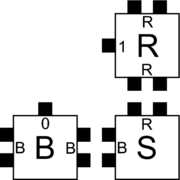
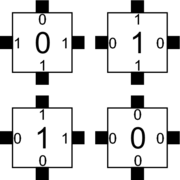
The aTAM is capable of Turing universal computation, so our first example will consist of a system which self-assembles a simple computation, namely an infinite binary counter.  The figure below shows three tile types which will be used to form the boundary of the counter on its bottom and right sides.  The figure below shows the additional $4$ tile types needed to perform the actual counting and to display, via their labels, the bits of each number.  We will define our binary counter tile assembly system as $\mathcal{T} = \{T,(S,(0,0)), 2\}$, that is, it will consist of tile set $T$ which will contain all $7$ of the tile types defined in the figure below, it will have a seed consisting of a single copy of a tile of type $S$ placed at position $(0,0)$, and it will be a temperature $2$ system (meaning that free tiles need to bind with at least a single strength-$2$ glue or two individual strength-$1$ glues on tiles within an existing assembly in order to attach to that assembly).
 +
{{multiple image
 +
| align = center
 +
| width = 180
 +
| footer = This tile set, seeded with the ''S'' tile at τ=2, self-assembles into an infinite binary counter.
 +
| image1 = Counter-border-tiles.png
 +
| alt1 = Sierpinski Growth Error
 +
| caption1 = The tile types which form the border of the counter
 +
| image2 = counter-rule-tiles.png
 +
| alt2 = Red cartouche
 +
| caption2 = The "rule" tile types which compute and represent the values of the counter
 +
}}
 +
 +
 +
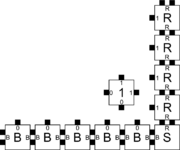
The figure below shows a small portion of the infinite assembly produced by $\mathcal{T}$.  In the figure below, the beginning of the formation of the border is shown.  Starting from $S$, border tiles $R$ can attach and form an infinite column upward using their strength-$2$ glues, and $B$ tiles can do the same to the left.  No rule tiles can attach until there are $2$ strength-$1$ bonds correctly positioned for them to bind to.  The figure below also shows the first rule tile which is about to attach into the corner.  In the figure below the bottom-right square of width and height $6$ of the infinite square assembly is shown.  Each horizontal row represents a single binary number in the counter, read from left to right (but which will have an infinite number of leading $0$'s to the left), and each row represents a binary number exactly one greater than the row immediately beneath it.  The computation is performed by the rule tiles which, essentially, receive as "input" a bit from beneath (representing the current value of that column) and a bit from the right (representing the carry bit being brought in from the bit position which is immediately less significant).  The labels and the northern glues of the rule tiles simply represent the (possibly new) "output" bit to be represented by that column (based on the two inputs), and the western glue represents the "output" carry bit which results.  The computation is possible because of the "cooperation" between two tiles providing input, enforced by the system parameter temperature $= 2$ and the single-strength glues of the rule tiles.
 +
 +
{{multiple image
 +
| align = center
 +
| width = 180
 +
| footer = Portions of the assembly formed by the binary counter.
 +
| image1 = counter-beginning.png
 +
| alt1 = Sierpinski Growth Error
 +
| caption1 = Border tiles can attach to the seed and form arbitrarily long bottom and right borders.  Rule tiles can bind only once two "inputs" are available.
 +
| image2 = counter-6x6.png
 +
| alt2 = Red cartouche
 +
| caption2 = A view of the 6 by 6 square of tiles at the bottom right corner of the assembly produced by the binary counter.  Note that the terminal assembly would actually continue infinitely far up and to the left.
 +
}}
 +
 +
==Survey of Results==
 +
 +
Results in the aTAM can often be mapped into two groups: 1. What can or can't self-assemble?, and 2. How hard is it to self-assemble a particular object?  Thus, sometimes the interest lies strictly in showing that something is possible or impossible, but often, even though we may know that something is possible, it turns out to be interesting to determine how efficiently it can be done.  The most common measure of efficiency is the number of unique tile types required, which can be thought of as the size of the "program" being used to direct the assembly. Finding optimally small tile sets which self-assemble into targeted shapes is of great interest, both theoretically and also for the sake of making potential laboratory implementations more feasible.  Another common measure is the scale factor.  Oftentimes it is possible to design tile sets with many fewer tile types which can self-assemble a target shape at a blown up scaling factor than it is to self-assemble the same shape without scaling it up.  Yet another measure may be assembly time.  Here are some results in the aTAM which seek to answer these and other questions.
 +
 +
*[[Building n by n squares]]
 +
*[[Building finite shapes]]
 +
*[[Building infinite shapes]]
 +
*[[Performing computations]]
 +
*[[Speed of assembly]]
 +
*[[The influence of temperature]]
 +
*[[Intrinsic Universality of the aTAM]]
 +
*[[Verification of aTAM systems]]
 +
*[[PATS problem and tile set generation]]
  
 +
==References==
 
<references>
 
<references>
  
Line 155: Line 198:
  
 
[[Category: Tile Assembly Models]]
 
[[Category: Tile Assembly Models]]
 +
[[Category:Self-assembly]]

Latest revision as of 11:11, 11 June 2019

Informal Description of the Model

The aTAM was developed to, in some sense, be an effectivization of Wang tiling. (See Wang Tiling for more about this relationship.) Namely, it provides a defined process by which an initial (called the seed) assembly can grow into a resultant structure. This is essentially accomplished by assigning a positive integer strength value to each edge color in a set of Wang tiles and stipulating that when two tile edges are adjacent, if their colors match then the edges bind with force equivalent to the strength of the edge color. Then, starting with a preformed seed assembly (usually taken to be a single tile of a specified type), additional tiles can attach one at a time as long as the sum of the strengths of the bonds that each makes with tiles already in the assembly meets a system wide threshold value called the temperature.

Formal Definition of the Model

\(\newcommand{\res}[1]{\textrm{res}(#1)}\) \(\newcommand{\termasm}[1]{\mathcal{A}_{\Box}[\mathcal{#1}]} \newcommand{\prodasm}[1]{\mathcal{A}[\mathcal{#1}]}\) We now give a brief formal definition of the aTAM. See [1] [2] [3] [4] for other developments of the model. Our notation is that of [4], which also contains a more complete definition.

Given a set \(T\) of tile types, an assembly is a partial function \({\alpha}:{\mathbb{Z}^2} \dashrightarrow {T}\). An assembly is \(\tau\)-stable if it cannot be broken up into smaller assemblies without breaking bonds of total strength at least \(\tau\), for some \(\tau \in \mathbb{N}\).

Self-assembly begins with a seed assembly \(\sigma\) and proceeds asynchronously and nondeterministically, with tiles adsorbing one at a time to the existing assembly in any manner that preserves \(\tau\)-stability at all times. A tile assembly system (TAS) is an ordered triple \(\mathcal{T} = (T, \sigma, \tau)\), where \(T\) is a finite set of tile types, \(\sigma\) is a seed assembly with finite domain, and \(\tau \in \mathbb{N}\). A generalized tile assembly system (GTAS) is defined similarly, but without the finiteness requirements. We write \(\mathcal{A}[\mathcal{T}]\) for the set of all assemblies that can arise (in finitely many steps or in the limit) from \(\mathcal{T}\). An assembly \(\alpha \in \mathcal{A}[\mathcal{T}]\) is terminal, and we write \(\alpha \in \mathcal{A}_{\Box}[\mathcal{T}]\), if no tile can be \(\tau\)-stably added to it. It is clear that \(\mathcal{A}_{\Box}[\mathcal{T}] \subset \mathcal{A}[\mathcal{T}]\).

An assembly sequence in a TAS \(\mathcal{T}\) is a (finite or infinite) sequence \(\vec{\alpha} = (\alpha_0,\alpha_1,\ldots)\) of assemblies in which each \(\alpha_{i+1}\) is obtained from \(\alpha_i\) by the addition of a single tile. The result \(\res{\vec{\alpha}}\) of such an assembly sequence is its unique limiting assembly. (This is the last assembly in the sequence if the sequence is finite.) The set \(\mathcal{A}[\mathcal{T}]\) is partially ordered by the relation \(\longrightarrow\) defined by

\(\) \begin{eqnarray*} \alpha \longrightarrow \alpha' & \textrm{iff} & \textrm{there is an assembly sequence } \vec{\alpha} = (\alpha_0,\alpha_1,\ldots) \\& & \textrm{such that } \alpha_0 = \alpha \textrm{ and } \alpha' = \res{\vec{\alpha}}.\\ \end{eqnarray*} \(\)

We say that \(\mathcal{T}\) is directed if the relation \(\longrightarrow\) is directed, i.e., if for all \(\alpha,\alpha' \in \prodasm{T}\), there exists \(\alpha'' \in \prodasm{T}\) such that \(\alpha \longrightarrow \alpha''\) and \(\alpha' \longrightarrow \alpha''\). It is easy to show that \(\mathcal{T}\) is directed if and only if there is a unique terminal assembly \(\alpha \in \mathcal{A}[\mathcal{T}]\) such that \(\sigma \longrightarrow \alpha\).

In general, even a directed TAS may have a very large (perhaps uncountably infinite) number of different assembly sequences leading to its terminal assembly. This seems to make it very difficult to prove that a TAS is directed. Fortunately, Soloveichik and Winfree [5] have defined a property, local determinism, of assembly sequences and proven the remarkable fact that, if a TAS \(\mathcal{T}\) has any assembly sequence that is locally deterministic, then \(\mathcal{T}\) is directed. Intuitively, an assembly sequence \(\vec{\alpha}\) is locally deterministic if (1) each tile added in \(\vec{\alpha}\) "just barely" binds to the existing assembly (meaning that is does so with a summed strength of bonds equal to exactly \(\tau\)); (2) if a tile of type \(t_0\) at a location \(\vec{m}\) and its immediate "output-neighbors" (i.e. those adjacent tiles which bound after the tile at \(\vec{m}\)) are deleted from the result of \(\vec{\alpha}\), then no tile of type \(t \ne t_0\) can attach itself to the thus-obtained configuration at location \(\vec{m}\); and (3) the result of \(\vec{\alpha}\) is terminal.


A set \(X \in \mathbb{Z}^2\) weakly self-assembles if there exists a TAS \({\mathcal T} = (T, \sigma, \tau)\) and a set \(B \subseteq T\) such that \(\alpha^{-1}(B) = X\) holds for every terminal assembly \(\alpha \in \termasm{T}\). Essentially, weak self-assembly can be thought of as the creation (or "painting") of a pattern of tiles from \(B\) (usually taken to be a unique "color") on a possibly larger "canvas" of un-colored tiles.

A set \(X\) strictly self-assembles if there is a TAS \(\mathcal{T}\) for which every assembly \(\alpha \in \mathcal{A}_{\Box}[\mathcal{T}]\) satisfies \(\dom \alpha = X\). Essentially, strict self-assembly means that tiles are only placed in positions defined by the shape. Note that if \(X\) strictly self-assembles, then \(X\) weakly self-assembles. (Let all tiles be in \(B\).)

An example tile that has glue of strength 0 on the left (W) and bottom (S), glue of color 'a' and strength 2 on the top (N), and glue of color 'b' and strength 1 on the right (E). This tile also has label 'L'..

Tiles are often depicted as squares whose various sides contain 0, 1, or 2 attached black squares, indicating whether the glue strengths on these sides are 0, 1, or 2, respectively. Thus, for example, a tile of the type shown to the right has glue of strength 0 on the left (W) and bottom (S), glue of color 'a' and strength 2 on the top (N), and glue of color 'b' and strength 1 on the right (E). This tile also has a label `L', which plays no formal role but may aid our understanding and discussion of the construction.


Example: A Binary Counter

The aTAM is capable of Turing universal computation, so our first example will consist of a system which self-assembles a simple computation, namely an infinite binary counter. The figure below shows three tile types which will be used to form the boundary of the counter on its bottom and right sides. The figure below shows the additional \(4\) tile types needed to perform the actual counting and to display, via their labels, the bits of each number. We will define our binary counter tile assembly system as \(\mathcal{T} = \{T,(S,(0,0)), 2\}\), that is, it will consist of tile set \(T\) which will contain all \(7\) of the tile types defined in the figure below, it will have a seed consisting of a single copy of a tile of type \(S\) placed at position \((0,0)\), and it will be a temperature \(2\) system (meaning that free tiles need to bind with at least a single strength-\(2\) glue or two individual strength-\(1\) glues on tiles within an existing assembly in order to attach to that assembly).

Sierpinski Growth Error
The tile types which form the border of the counter
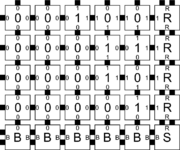
Red cartouche
The "rule" tile types which compute and represent the values of the counter
This tile set, seeded with the S tile at τ=2, self-assembles into an infinite binary counter.


The figure below shows a small portion of the infinite assembly produced by \(\mathcal{T}\). In the figure below, the beginning of the formation of the border is shown. Starting from \(S\), border tiles \(R\) can attach and form an infinite column upward using their strength-\(2\) glues, and \(B\) tiles can do the same to the left. No rule tiles can attach until there are \(2\) strength-\(1\) bonds correctly positioned for them to bind to. The figure below also shows the first rule tile which is about to attach into the corner. In the figure below the bottom-right square of width and height \(6\) of the infinite square assembly is shown. Each horizontal row represents a single binary number in the counter, read from left to right (but which will have an infinite number of leading \(0\)'s to the left), and each row represents a binary number exactly one greater than the row immediately beneath it. The computation is performed by the rule tiles which, essentially, receive as "input" a bit from beneath (representing the current value of that column) and a bit from the right (representing the carry bit being brought in from the bit position which is immediately less significant). The labels and the northern glues of the rule tiles simply represent the (possibly new) "output" bit to be represented by that column (based on the two inputs), and the western glue represents the "output" carry bit which results. The computation is possible because of the "cooperation" between two tiles providing input, enforced by the system parameter temperature \(= 2\) and the single-strength glues of the rule tiles.

Sierpinski Growth Error
Border tiles can attach to the seed and form arbitrarily long bottom and right borders. Rule tiles can bind only once two "inputs" are available.
Red cartouche
A view of the 6 by 6 square of tiles at the bottom right corner of the assembly produced by the binary counter. Note that the terminal assembly would actually continue infinitely far up and to the left.
Portions of the assembly formed by the binary counter.

Survey of Results

Results in the aTAM can often be mapped into two groups: 1. What can or can't self-assemble?, and 2. How hard is it to self-assemble a particular object? Thus, sometimes the interest lies strictly in showing that something is possible or impossible, but often, even though we may know that something is possible, it turns out to be interesting to determine how efficiently it can be done. The most common measure of efficiency is the number of unique tile types required, which can be thought of as the size of the "program" being used to direct the assembly. Finding optimally small tile sets which self-assemble into targeted shapes is of great interest, both theoretically and also for the sake of making potential laboratory implementations more feasible. Another common measure is the scale factor. Oftentimes it is possible to design tile sets with many fewer tile types which can self-assemble a target shape at a blown up scaling factor than it is to self-assemble the same shape without scaling it up. Yet another measure may be assembly time. Here are some results in the aTAM which seek to answer these and other questions.

References

  1. ↑ Erik Winfree - Algorithmic Self-Assembly of DNA
    Ph.D. Thesis, California Institute of Technology , June 1998
    Bibtex
    Author : Erik Winfree
    Title : Algorithmic Self-Assembly of DNA
    In : Ph.D. Thesis, California Institute of Technology -
    Address :
    Date : June 1998
  2. ↑ Paul W. K. Rothemund, Erik Winfree - The Program-size Complexity of Self-Assembled Squares (extended abstract)
    STOC '00: Proceedings of the thirty-second annual ACM Symposium on Theory of Computing pp. 459--468, Portland, Oregon, United States,2000
    Bibtex
    Author : Paul W. K. Rothemund, Erik Winfree
    Title : The Program-size Complexity of Self-Assembled Squares (extended abstract)
    In : STOC '00: Proceedings of the thirty-second annual ACM Symposium on Theory of Computing -
    Address : Portland, Oregon, United States
    Date : 2000
  3. ↑ Paul W. K. Rothemund - Theory and Experiments in Algorithmic Self-Assembly
    Ph.D. Thesis, University of Southern California , December 2001
    Bibtex
    Author : Paul W. K. Rothemund
    Title : Theory and Experiments in Algorithmic Self-Assembly
    In : Ph.D. Thesis, University of Southern California -
    Address :
    Date : December 2001
  4. ↑ 4.0 4.1 James I. Lathrop, Jack H. Lutz, Scott M. Summers - Strict Self-Assembly of Discrete Sierpinski Triangles
    Theoretical Computer Science 410:384--405,2009
    Bibtex
    Author : James I. Lathrop, Jack H. Lutz, Scott M. Summers
    Title : Strict Self-Assembly of Discrete Sierpinski Triangles
    In : Theoretical Computer Science -
    Address :
    Date : 2009
  5. ↑ David Soloveichik, Erik Winfree - Complexity of Self-Assembled Shapes
    SIAM Journal on Computing 36(6):1544-1569,2007
    Bibtex
    Author : David Soloveichik, Erik Winfree
    Title : Complexity of Self-Assembled Shapes
    In : SIAM Journal on Computing -
    Address :
    Date : 2007
Retrieved from "http://self-assembly.net/wiki/index.php?title=Abstract_Tile_Assembly_Model_(aTAM)&oldid=1529"