Difference between revisions of "Zig-Zag Systems"
| (3 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
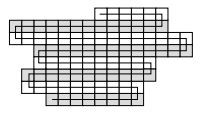
A tile assembly system $\mathcal{T} = (T, \sigma, 2)$ is called a zig-zag tile assembly system if (1) $\mathcal{T}$ is directed, (2) there is a single assembly sequence $\vec{\alpha}$ in $\mathcal{T}$ , with $A_t[\mathcal{T}] = {\alpha}$, and (3) for every $\vec{x} \in$ dom $\alpha$, (0, 1) $\notin $IN$^{\vec{\alpha}} (\vec{x})$. Intuitively, zig-zag systems are those that grow one horizontal row at a time, alternating left-to-right and right-to-left growth, always adding new rows to the north and never growing south. Zig-zag systems are capable of simulating universal Turing machines, and thus universal computation. If $\mathcal{T}$ is a zig-zag system with $A_t[\mathcal{T}] = {\alpha}$ and for every $\vec{x} \in$ dom $\alpha$ and every $\vec{u} \in U_2,$ $str_{α(\vec{x})}(\vec{U})$ + $str_{α(\vec{x})}(-\vec{U})$ < 4, then we say that $\mathcal{T}$ is compact. Intuitively, compact zig-zag systems are zig-zag systems that only extend the width of each row by one over the length of the previous row, and only grow upward by one tile before continuing horizontal growth. Compact zig-zag systems are capable of simulating universal Turing machines. <ref name="NegaGlue"/> | A tile assembly system $\mathcal{T} = (T, \sigma, 2)$ is called a zig-zag tile assembly system if (1) $\mathcal{T}$ is directed, (2) there is a single assembly sequence $\vec{\alpha}$ in $\mathcal{T}$ , with $A_t[\mathcal{T}] = {\alpha}$, and (3) for every $\vec{x} \in$ dom $\alpha$, (0, 1) $\notin $IN$^{\vec{\alpha}} (\vec{x})$. Intuitively, zig-zag systems are those that grow one horizontal row at a time, alternating left-to-right and right-to-left growth, always adding new rows to the north and never growing south. Zig-zag systems are capable of simulating universal Turing machines, and thus universal computation. If $\mathcal{T}$ is a zig-zag system with $A_t[\mathcal{T}] = {\alpha}$ and for every $\vec{x} \in$ dom $\alpha$ and every $\vec{u} \in U_2,$ $str_{α(\vec{x})}(\vec{U})$ + $str_{α(\vec{x})}(-\vec{U})$ < 4, then we say that $\mathcal{T}$ is compact. Intuitively, compact zig-zag systems are zig-zag systems that only extend the width of each row by one over the length of the previous row, and only grow upward by one tile before continuing horizontal growth. Compact zig-zag systems are capable of simulating universal Turing machines. <ref name="NegaGlue"/> | ||
| − | <ref name="ZZSim"/> | + | [[File:zig_zag.jpg|center|350px|An example of a zig-zag system]] |
| + | |||
| + | In a paper by Cook, Fu, and Schweller<ref name="ZZSim"/>, it is shown that 2D zig-zag systems at temperature 2 can be simulated by 3D zig-zag systems in temperature 1. Their result is as follows: for any 2 dimensional temperature 2 zig-zag tile system $\Gamma = (T, s, 2)$ with $\sigma_T$ denoting the set of distinct strength 1 north / south glue types occurring in $T$, there exists a 3D temperature 1 tile system that simulates $\Gamma$ at vertical scale = 4, horizontal scale = $O(log |\sigma_T|)$, and (total) tile complexity $O(|T| log |\sigma_T|)$, which constitutes a $O(log |\sigma_T|)$ tile complexity scale factor. | ||
| + | |||
| + | |||
| + | In order to simulate a temperature 2 zig-zag tileset with a temperature 1 tileset, the construction replaces each tile type in the original system with a collection of tiles designed to assemble a larger macro tile at temperature 1. The goal is to “fake” cooperative temperature 2 attachment of a given tile from the original system by utilizing geometry to force an otherwise non-deterministic growth of tiles to read the north input glue of a given macro tile. | ||
| + | |||
| + | |||
| + | The same paper<ref name="ZZSim"/> also gives proof that a 2D zig-zag system at temperature 2 can be simulated by a probabilistic 2D zig-zag system at temperature 1. That result is as follows: The basic idea is similar to the 3D conversion. Each tile type for a given east glue x is used to generate a binary tree of nondeterministic chains of tiles to decode a southern input glue encoded by geometry. However, in 2D, it is not possible to block both branches of the binary tree due to planarity. Therefore, we only block one side or block neither side. | ||
| + | |||
| + | |||
| + | Probabilistic bit readers work by spawning a short path and a long path that represent the two different bits that can be read. To write a one, the bit writer blocks the short path, only allowing the long path to grow. To write a zero, the bit writer blocks neither path. However, since the short path requires fewer tiles than the long path does, it is probable that the short path will beat the long path and block the long path from growing. | ||
| + | |||
==References== | ==References== | ||
Latest revision as of 11:07, 15 July 2016
Overview
A tile assembly system \(\mathcal{T} = (T, \sigma, 2)\) is called a zig-zag tile assembly system if (1) \(\mathcal{T}\) is directed, (2) there is a single assembly sequence \(\vec{\alpha}\) in \(\mathcal{T}\) , with \(A_t[\mathcal{T}] = {\alpha}\), and (3) for every \(\vec{x} \in\) dom \(\alpha\), (0, 1) \(\notin \)IN\(^{\vec{\alpha}} (\vec{x})\). Intuitively, zig-zag systems are those that grow one horizontal row at a time, alternating left-to-right and right-to-left growth, always adding new rows to the north and never growing south. Zig-zag systems are capable of simulating universal Turing machines, and thus universal computation. If \(\mathcal{T}\) is a zig-zag system with \(A_t[\mathcal{T}] = {\alpha}\) and for every \(\vec{x} \in\) dom \(\alpha\) and every \(\vec{u} \in U_2,\) \(str_{α(\vec{x})}(\vec{U})\) + \(str_{α(\vec{x})}(-\vec{U})\) < 4, then we say that \(\mathcal{T}\) is compact. Intuitively, compact zig-zag systems are zig-zag systems that only extend the width of each row by one over the length of the previous row, and only grow upward by one tile before continuing horizontal growth. Compact zig-zag systems are capable of simulating universal Turing machines. [1]
In a paper by Cook, Fu, and Schweller[2], it is shown that 2D zig-zag systems at temperature 2 can be simulated by 3D zig-zag systems in temperature 1. Their result is as follows: for any 2 dimensional temperature 2 zig-zag tile system \(\Gamma = (T, s, 2)\) with \(\sigma_T\) denoting the set of distinct strength 1 north / south glue types occurring in \(T\), there exists a 3D temperature 1 tile system that simulates \(\Gamma\) at vertical scale = 4, horizontal scale = \(O(log |\sigma_T|)\), and (total) tile complexity \(O(|T| log |\sigma_T|)\), which constitutes a \(O(log |\sigma_T|)\) tile complexity scale factor.
In order to simulate a temperature 2 zig-zag tileset with a temperature 1 tileset, the construction replaces each tile type in the original system with a collection of tiles designed to assemble a larger macro tile at temperature 1. The goal is to “fake” cooperative temperature 2 attachment of a given tile from the original system by utilizing geometry to force an otherwise non-deterministic growth of tiles to read the north input glue of a given macro tile.
The same paper[2] also gives proof that a 2D zig-zag system at temperature 2 can be simulated by a probabilistic 2D zig-zag system at temperature 1. That result is as follows: The basic idea is similar to the 3D conversion. Each tile type for a given east glue x is used to generate a binary tree of nondeterministic chains of tiles to decode a southern input glue encoded by geometry. However, in 2D, it is not possible to block both branches of the binary tree due to planarity. Therefore, we only block one side or block neither side.
Probabilistic bit readers work by spawning a short path and a long path that represent the two different bits that can be read. To write a one, the bit writer blocks the short path, only allowing the long path to grow. To write a zero, the bit writer blocks neither path. However, since the short path requires fewer tiles than the long path does, it is probable that the short path will beat the long path and block the long path from growing.