Difference between revisions of "Building infinite shapes"
Jhendricks (talk | contribs) (→Building infinite shapes) |
|||
| (9 intermediate revisions by 2 users not shown) | |||
| Line 5: | Line 5: | ||
As it has been shown that any finite shape can self-assemble in the aTAM, in order to test the limits of the model and find shapes which are impossible to self-assemble, it is necessary to look at infinite shapes. While the self-assembly of infinite shapes may not have typical practical (i.e. physical, laboratory) applications, the study provides insights into fundamental limitations of self-assembling systems, in particular regarding their ability to propagate information through the growth fronts of assemblies. | As it has been shown that any finite shape can self-assemble in the aTAM, in order to test the limits of the model and find shapes which are impossible to self-assemble, it is necessary to look at infinite shapes. While the self-assembly of infinite shapes may not have typical practical (i.e. physical, laboratory) applications, the study provides insights into fundamental limitations of self-assembling systems, in particular regarding their ability to propagate information through the growth fronts of assemblies. | ||
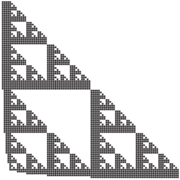
| − | Due to their complex, aperiodic nature, discrete self-similar fractals have provided an interesting set of infinite shapes to explore. In <ref name=jSSADST/>, Lathrop, Lutz, and Summers showed that it is impossible for the discrete Sierpinski triangle (see | + | Due to their complex, aperiodic nature, discrete self-similar fractals have provided an interesting set of infinite shapes to explore. In <ref name=jSSADST/>, Lathrop, Lutz, and Summers showed that it is impossible for the discrete Sierpinski triangle (see first image in the figure below) to strictly self-assemble in the aTAM (at any temperature). Note that this is in contrast to the fact that it can weakly self-assemble, with a very simple tile set of 7 tile types. The proof relies on the fact that at each successive stage, as the stages of the fractal structure grow larger, each is connected to the rest of the assembly by a single tile. Since there are an infinite number of stages, all of different sizes, it is impossible for the single tiles connecting each of them to the assembly to transmit the information about how large the newly forming stage should be, and thus it is impossible for the fractal to self-assemble. Patitz and Summers <ref name=jSADSSF/> extended this proof technique to cover a class of similar fractals. It is conjectured by the author of this paper that no discrete self-similar fractal strictly self-assembles in the aTAM, but that remains an open question. |
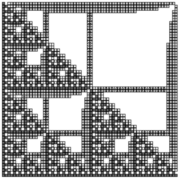
| − | Despite the impossibility of strictly self-assembling the discrete Sierpinski triangle, in <ref name=jSSADST/> it was shown that an approximation of that fractal, which the authors called the ''fibered'' Sierpinski triangle, does in fact strictly self-assemble. The fibered version is simply a rough visual approximation of the original but with one additional row and column of tiles added to each subsequent stage of the fractal during assembly (see | + | {{multiple image |
| + | | align = center | ||
| + | | width = 180 | ||
| + | | footer = Various patterns corresponding to the Sierpinski triangle | ||
| + | | image1 = Sierpinski-triangle.png | ||
| + | | alt1 = A portion of the discrete Sierpinski triangle | ||
| + | | caption1 = The tile types which form the border of the counter | ||
| + | | image2 = Sierpinski-fibered.png | ||
| + | | alt2 = Red cartouche | ||
| + | | caption2 = A portion of the approximate Sierpinski triangle of <ref name=jSSADST/> | ||
| + | | image3 = Sierpinski-laced.png | ||
| + | | alt3 = Red cartouche | ||
| + | | caption3 = A portion of the approximate Sierpinski triangle of <ref name=LutzShutters12/> | ||
| + | }} | ||
| + | |||
| + | Despite the impossibility of strictly self-assembling the discrete Sierpinski triangle, in <ref name=jSSADST/> it was shown that an approximation of that fractal, which the authors called the ''fibered'' Sierpinski triangle, does in fact strictly self-assemble. The fibered version is simply a rough visual approximation of the original but with one additional row and column of tiles added to each subsequent stage of the fractal during assembly (see second image in the above figure). Not only does the approximation look similar to the original, it was shown to have the same fractal (or zeta) dimension. In <ref name=jSADSSF/>, the fibering construction was extended to an entire class of fractals. Along a similar line, Shutters and Lutz <ref name=LutzShutters12/> showed that a different type of approximation of the Sierpinski triangle strictly self-assembles. This approximation also retains the same approximate appearance and fractal dimension, but instead of "spreading" out successive stages of the fractal with fibering, it utilizes a small portion of each hole in the definition of the shape (see third image in the above figure). In <ref name=KautzShutters11/> Kautz and Shutters further extended this construction to an entire class of fractals. | ||
Similar to their result about finite shapes mentioned in Section~\ref{sec:finite-shapes}, in <ref name=BryChiDotKarSek10/> Bryans, Chiniforooshan, Doty, Kari, and Seki also showed a result about the power of nondeterminism in forming infinite structures, proving that there exist infinite shapes which can ''only'' self-assemble in non-deterministic systems. This means that no deterministic system is able to self-assemble such shapes, and is a further testament to the fact that nondeterminism is a source of increased power in the aTAM. | Similar to their result about finite shapes mentioned in Section~\ref{sec:finite-shapes}, in <ref name=BryChiDotKarSek10/> Bryans, Chiniforooshan, Doty, Kari, and Seki also showed a result about the power of nondeterminism in forming infinite structures, proving that there exist infinite shapes which can ''only'' self-assemble in non-deterministic systems. This means that no deterministic system is able to self-assemble such shapes, and is a further testament to the fact that nondeterminism is a source of increased power in the aTAM. | ||
| + | |||
| + | ==How to Build the Discrete Sierpinski Triangle in the STAM== | ||
| + | |||
| + | In a paper by Hendricks, Olsen, Patitz, Rogers, and Thomas<ref name=SierSignal/>, it is shown that the infinite Sierpinski triangle can be assembled in the STAM. Their result is as follows. | ||
| + | |||
| + | Theorem 1. There exists an STAM system T∆ = (T, 1) such that T∆ has exactly one infinite terminal supertile α∆, and dom (α∆) = S∆, i.e. is exactly the discrete Sierpinski triangle, and for all α ∈ A✷[T ] such that α 6= α∆, |dom (α)| ≤ 4. | ||
| + | |||
| + | This construction uses the ability of signal passing tiles in the STAM to turn off their glues and allow for pieces of the assembly to break away after they helped to assemble pieces of the shape. | ||
==References== | ==References== | ||
| + | <references> | ||
| + | |||
| + | <ref name =BryChiDotKarSek10><bibtex> | ||
| + | @inproceedings{BryChiDotKarSek10, | ||
| + | author = {Nathaniel Bryans, Ehsan Chiniforooshan, David Doty, Lila Kari, and Shinnosuke Seki}, | ||
| + | title = {The power of nondeterminism in self-assembly}, | ||
| + | booktitle = {SODA 2011: Proceedings of the 22nd Annual ACM-SIAM Symposium on Discrete Algorithms}, | ||
| + | year = {2011}, | ||
| + | pages = {590--602}, | ||
| + | publisher = {SIAM} | ||
| + | } | ||
| + | </bibtex></ref> | ||
| + | |||
| + | <ref name =jSSADST><bibtex> | ||
| + | @article{jSSADST, | ||
| + | author = "James I. Lathrop and Jack H. Lutz and Scott M. Summers", | ||
| + | title = "Strict Self-Assembly of Discrete Sierpinski Triangles", | ||
| + | journal = "Theoretical Computer Science", | ||
| + | volume = "410", | ||
| + | year = "2009", | ||
| + | pages = "384--405" | ||
| + | } | ||
| + | note = "Preliminary version appeared in Proceedings of The Third Conference on Computability in Europe (Siena, Italy, June 18-23, 2007)" | ||
| + | </bibtex></ref> | ||
| + | |||
| + | <ref name =jSADSSF><bibtex> | ||
| + | @article{jSADSSF, | ||
| + | author = {Matthew J. Patitz and Scott M. Summers}, | ||
| + | title = {Self-assembly of discrete self-similar fractals}, | ||
| + | journal = {Natural Computing}, | ||
| + | volume = {1} | ||
| + | year = {2010}, | ||
| + | pages = {135--172}, | ||
| + | |||
| + | } | ||
| + | </bibtex></ref> | ||
| + | |||
| + | <ref name =LutzShutters12><bibtex> | ||
| + | @article{LutzShutters12, | ||
| + | author = {Jack H. Lutz and Brad Shutters}, | ||
| + | title = {Approximate self-assembly of the sierpinski triangle}, | ||
| + | journal = {Theory Comput. Syst.}, | ||
| + | volume = {51} | ||
| + | number {3} | ||
| + | year = {2012}, | ||
| + | pages = {372--400}, | ||
| + | |||
| + | } | ||
| + | </bibtex></ref> | ||
| + | |||
| + | <ref name =KautzShutters11><bibtex> | ||
| + | @article{KautzShutters11, | ||
| + | author = {Steven M. Kautz and Brad Shutters}, | ||
| + | title = {Self-assembling rulers for approximating generalized sierpinski carpets}, | ||
| + | journal = {Lecture Notes in Computer Science}, | ||
| + | volume = {6842} | ||
| + | year = {2011}, | ||
| + | pages = {284--296}, | ||
| + | |||
| + | } | ||
| + | </bibtex></ref> | ||
| + | |||
| + | <ref name =SierSignal><bibtex> | ||
| + | @article{SierpinskiSignal, | ||
| + | author = {Jacob Hendricks, Meagan Olsen, Matthew J. Patitz, Trent A. Rogers, and Hadley Thomas}, | ||
| + | title = {Hierarchical Self-Assembly of Fractals with Signal-Passing Tiles}, | ||
| + | journal = {DNA 22}, | ||
| + | year = {2016}, | ||
| + | } | ||
| + | </bibtex></ref> | ||
| + | </references> | ||
[[Category:Results in the aTAM]] | [[Category:Results in the aTAM]] | ||
| + | [[Category:Self-assembly]] | ||
Latest revision as of 13:49, 21 June 2016
Contents
Building infinite shapes
As it has been shown that any finite shape can self-assemble in the aTAM, in order to test the limits of the model and find shapes which are impossible to self-assemble, it is necessary to look at infinite shapes. While the self-assembly of infinite shapes may not have typical practical (i.e. physical, laboratory) applications, the study provides insights into fundamental limitations of self-assembling systems, in particular regarding their ability to propagate information through the growth fronts of assemblies.
Due to their complex, aperiodic nature, discrete self-similar fractals have provided an interesting set of infinite shapes to explore. In [1], Lathrop, Lutz, and Summers showed that it is impossible for the discrete Sierpinski triangle (see first image in the figure below) to strictly self-assemble in the aTAM (at any temperature). Note that this is in contrast to the fact that it can weakly self-assemble, with a very simple tile set of 7 tile types. The proof relies on the fact that at each successive stage, as the stages of the fractal structure grow larger, each is connected to the rest of the assembly by a single tile. Since there are an infinite number of stages, all of different sizes, it is impossible for the single tiles connecting each of them to the assembly to transmit the information about how large the newly forming stage should be, and thus it is impossible for the fractal to self-assemble. Patitz and Summers [2] extended this proof technique to cover a class of similar fractals. It is conjectured by the author of this paper that no discrete self-similar fractal strictly self-assembles in the aTAM, but that remains an open question.
Despite the impossibility of strictly self-assembling the discrete Sierpinski triangle, in [1] it was shown that an approximation of that fractal, which the authors called the fibered Sierpinski triangle, does in fact strictly self-assemble. The fibered version is simply a rough visual approximation of the original but with one additional row and column of tiles added to each subsequent stage of the fractal during assembly (see second image in the above figure). Not only does the approximation look similar to the original, it was shown to have the same fractal (or zeta) dimension. In [2], the fibering construction was extended to an entire class of fractals. Along a similar line, Shutters and Lutz [3] showed that a different type of approximation of the Sierpinski triangle strictly self-assembles. This approximation also retains the same approximate appearance and fractal dimension, but instead of "spreading" out successive stages of the fractal with fibering, it utilizes a small portion of each hole in the definition of the shape (see third image in the above figure). In [4] Kautz and Shutters further extended this construction to an entire class of fractals.
Similar to their result about finite shapes mentioned in Section~\ref{sec:finite-shapes}, in [5] Bryans, Chiniforooshan, Doty, Kari, and Seki also showed a result about the power of nondeterminism in forming infinite structures, proving that there exist infinite shapes which can only self-assemble in non-deterministic systems. This means that no deterministic system is able to self-assemble such shapes, and is a further testament to the fact that nondeterminism is a source of increased power in the aTAM.
How to Build the Discrete Sierpinski Triangle in the STAM
In a paper by Hendricks, Olsen, Patitz, Rogers, and Thomas[6], it is shown that the infinite Sierpinski triangle can be assembled in the STAM. Their result is as follows.
Theorem 1. There exists an STAM system T∆ = (T, 1) such that T∆ has exactly one infinite terminal supertile α∆, and dom (α∆) = S∆, i.e. is exactly the discrete Sierpinski triangle, and for all α ∈ A✷[T ] such that α 6= α∆, |dom (α)| ≤ 4.
This construction uses the ability of signal passing tiles in the STAM to turn off their glues and allow for pieces of the assembly to break away after they helped to assemble pieces of the shape.
References
- ↑ 1.0 1.1 1.2
James I. Lathrop, Jack H. Lutz, Scott M. Summers - Strict Self-Assembly of Discrete Sierpinski Triangles
- Theoretical Computer Science 410:384--405,2009
- BibtexAuthor : James I. Lathrop, Jack H. Lutz, Scott M. Summers
Title : Strict Self-Assembly of Discrete Sierpinski Triangles
In : Theoretical Computer Science -
Address :
Date : 2009
- ↑ 2.0 2.1
Matthew J. Patitz, Scott M. Summers - Self-assembly of discrete self-similar fractals
- ↑ 3.0 3.1
Jack H. Lutz, Brad Shutters - Approximate self-assembly of the sierpinski triangle
- ↑
Steven M. Kautz, Brad Shutters - Self-assembling rulers for approximating generalized sierpinski carpets
- Lecture Notes in Computer Science 6842:284--296,2011
- BibtexAuthor : Steven M. Kautz, Brad Shutters
Title : Self-assembling rulers for approximating generalized sierpinski carpets
In : Lecture Notes in Computer Science -
Address :
Date : 2011
- ↑
Nathaniel Bryans, Ehsan Chiniforooshan, David Doty, Lila Kari,, Shinnosuke Seki - The power of nondeterminism in self-assembly
- SODA 2011: Proceedings of the 22nd Annual ACM-SIAM Symposium on Discrete Algorithms pp. 590--602,2011
- BibtexAuthor : Nathaniel Bryans, Ehsan Chiniforooshan, David Doty, Lila Kari,, Shinnosuke Seki
Title : The power of nondeterminism in self-assembly
In : SODA 2011: Proceedings of the 22nd Annual ACM-SIAM Symposium on Discrete Algorithms -
Address :
Date : 2011
- ↑
Jacob Hendricks, Meagan Olsen, Matthew J. Patitz, Trent A. Rogers,, Hadley Thomas - Hierarchical Self-Assembly of Fractals with Signal-Passing Tiles