Difference between revisions of "Kinetic Tile Assembly Model (kTAM)"
(→Error Types) |
|||
| (26 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
==Model Definition== | ==Model Definition== | ||
| − | In the kTAM <ref name=Winf98 /> <ref name=WinBek03 /> <ref name=FujZhaWinMur08 />, a monomer tile can be added to the assembly with some association (forward) rate, or removed from the assembly with some dissociation (reverse) rate. Similar to the [[Abstract Tile Assembly Model (aTAM) | aTAM]], only the singleton tiles are allowed to attach to, and in this case detach from, a seeded assembly. These rates are denoted by $r_f$ and $r_{r,b}$, respectively. At every available site on the perimeter of an assembly (i.e. the [[Frontier | frontier]]), every possible monomer tile can associate to the assembly, regardless of whether the monomer is correct or not (i.e. whether or not the glues match). The forward rate depends only on the monomer tile concentration, [ | + | In the kTAM <ref name=Winf98 /> <ref name=WinBek03 /> <ref name=FujZhaWinMur08 />, a monomer tile can be added to the assembly with some association (forward) rate, or removed from the assembly with some dissociation (reverse) rate. Similar to the [[Abstract Tile Assembly Model (aTAM) | aTAM]], only the singleton tiles are allowed to attach to, and in this case detach from, a seeded assembly. These rates are denoted by $r_f$ and $r_{r,b}$, respectively. At every available site on the perimeter of an assembly (i.e. the [[Growth Frontier | frontier]]), every possible monomer tile can associate to the assembly, regardless of whether the monomer is correct or not (i.e. whether or not the glues match). The forward rate depends only on the monomer tile concentration, $[monomer]$: |
| − | $\begin{eqnarray} | + | |
| − | + | $\begin{eqnarray*} r_f = k_f[monomer] = k_f e^{-G_{mc}} \end{eqnarray*}$ | |
| − | \end{eqnarray}$ | + | |
where $G_{mc} > 0$ is the non-dimensional entropic cost of associating to an assembly. In the kTAM, for simplicity it is assumed that tile concentrations remain constant at $[monomer] = e^{-G_{mc}}$. Therefore, since the forward rate constant $k_f$ is a constant, the entire forward rate $r_f$ is also constant. | where $G_{mc} > 0$ is the non-dimensional entropic cost of associating to an assembly. In the kTAM, for simplicity it is assumed that tile concentrations remain constant at $[monomer] = e^{-G_{mc}}$. Therefore, since the forward rate constant $k_f$ is a constant, the entire forward rate $r_f$ is also constant. | ||
The reverse rate is dependent upon the binding strength ''b'' of the tile to the assembly, and in fact the relationship is exponential: | The reverse rate is dependent upon the binding strength ''b'' of the tile to the assembly, and in fact the relationship is exponential: | ||
| − | $\begin{eqnarray} | + | |
| − | + | $\begin{eqnarray*} r_{r,b} = k_{r,b} = k_f e^{-bG_{se}} \end{eqnarray*}$ | |
| − | \end{eqnarray}$ | + | |
where $G_{se}$ is the non-dimensional free energy cost of breaking a single bond and ''b'' is the number of "single-strength" bonds the tile has made. | where $G_{se}$ is the non-dimensional free energy cost of breaking a single bond and ''b'' is the number of "single-strength" bonds the tile has made. | ||
| Line 20: | Line 20: | ||
Because the kTAM accurately models the behavior of DNA based tile self-assembly in the laboratory, most especially the common types of errors observed, it has provided an excellent foundation for work in error prevention and correction. | Because the kTAM accurately models the behavior of DNA based tile self-assembly in the laboratory, most especially the common types of errors observed, it has provided an excellent foundation for work in error prevention and correction. | ||
| + | ==Error Types== | ||
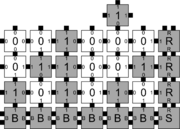
| + | In order to discuss the types of errors that can occur during self-assembly in the kTAM, we will refer to an example system which is designed to weakly self-assemble the Sierpinski triangle. See the figures to the right for details. | ||
| + | |||
| + | {{multiple image | ||
| + | | width = 180 | ||
| + | | image1 = Sierpinski-tiles.png | ||
| + | | alt1 = Sierpinski Growth Error | ||
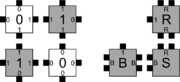
| + | | caption1 = The tile types for [[Weak Self-Assembly | weakly self-assembling]] the Sierpinski triangle. | ||
| + | | image2 = Sierpinski-correct.png | ||
| + | | alt2 = Red cartouche | ||
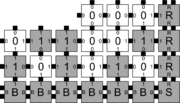
| + | | caption2 = A view of the 9 × 9 square of tiles at the bottom right corner of the weakly self-assembled Sierpinski triangle. Note that the terminal assembly would actually continue infinitely far up and to the left. | ||
| + | }} | ||
| + | |||
| + | The errors that occur during assembly can be divided into three general types: 1) [[Growth Errors | growth errors]] (or ''mismatch errors''), 2) [[Facet Errors | facet errors]], and 3) [[Nucleation Errors | nucleation errors]] <ref name=FujZhaWinMur08 />. A growth error, an example of which can be seen in the figures below, occurs when one or more sides of a tile which binds to an assembly have glues which do not match the adjacent glues (called glue mismatches). Such a tile may bind with insufficient strength to remain permanently bound, but before it has an opportunity to dissociate, a previously unoccupied neighboring position may be filled by a tile which binds without mismatches, thus resulting in an assembly where every tile has sufficient strength to remain permanently attached despite the mismatch. This essentially "locks" the incorrect tile into place and potentially allows assembly to proceed with an incorrectly placed tile which may cause further deviations from the desired shape or pattern. Somewhat similarly, a facet error also occurs on the edge of a growing assembly. A facet error (see figures below for an example) again occurs when a tile binds with insufficient strength for permanent attachment (but this time with no mismatches), and again is locked into place by a subsequent tile addition. The third type of errors, nucleation errors, occur when tiles aggregate with each other without any attachment to the seed structure, and thus 'seed' a new type of assembly. | ||
| + | |||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | |||
| + | {{multiple image | ||
| + | | align = left | ||
| + | | width = 180 | ||
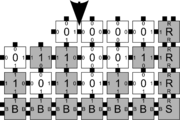
| + | | footer = Example growth error in the kTAM: a tile initially binds with insufficient strength due to a mismatch, but the error is then "locked in" by a tile which arrives later. | ||
| + | | image1 = Sierpinski-growth-error1.png | ||
| + | | alt1 = Sierpinski Growth Error | ||
| + | | caption1 = A partial assembly which is error-free. | ||
| + | | image2 = Sierpinski-growth-error2.png | ||
| + | | alt2 = Red cartouche | ||
| + | | caption2 = The binding of a tile with one glue match and one mismatch (shown by arrow). | ||
| + | | image3 = Sierpinski-growth-error3.png | ||
| + | | alt3 = not sure | ||
| + | | caption3 = Before the erroneously attached tile can detach, another tile (shown by arrow) attaches with 2 matching bonds so that all tiles are now connected by two correctly formed bonds | ||
| + | }} | ||
| + | |||
| + | {{multiple image | ||
| + | | align = right | ||
| + | | width = 180 | ||
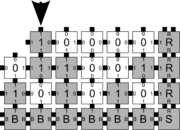
| + | | footer = Example facet error in the kTAM | ||
| + | | image1 = Sierpinski-facet-error1.png | ||
| + | | alt1 = Sierpinski Growth Error | ||
| + | | caption1 = A partial assembly which is error-free. | ||
| + | | image2 = Sierpinski-facet-error2.png | ||
| + | | alt2 = Red cartouche | ||
| + | | caption2 = The binding of a tile via a single glue. | ||
| + | | image3 = Sierpinski-growth-error3.png | ||
| + | | alt3 = not sure | ||
| + | | caption3 = Before the erroneously attached tile can detach, another tile attaches with 2 matching bonds so that all tiles are now connected by two correctly formed bonds | ||
| + | }} | ||
| + | |||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | |||
| + | ==Survey of Results== | ||
| + | The ability of the kTAM to accurately model the errors seen in laboratory settings coupled with its clean theoretical definition make it an ideal model in which to study mechanisms of error prevention and correction. Additionally, the algorithmic nature of self-assembly in the kTAM provides the opportunity to effectively apply a variety of algorithms from seemingly unrelated fields such as data transmission to make kTAM systems more robust. | ||
| + | |||
| + | While simply adjusting the ratio of $G_{mc}$ to $G_{se}$ is sufficient to drive error rates arbitrarily low, that comes at the cost of a huge slow-down to the overall assembly process. The pages below consists of results which are focused on one or both of the dual goals of decreasing the rate of errors during assembly and minimizing assembly time. | ||
| + | |||
| + | [[Error Suppresion Via Block Replacement]] | ||
| + | |||
| + | [[Facet Error Handling]] | ||
| + | |||
| + | [[Snaked Proofreading]] | ||
| + | |||
| + | [[Self-Healing]] | ||
| + | |||
| + | [[Enhanced Tile Design]] | ||
| + | [[Controlling Nucleation]] | ||
==References== | ==References== | ||
| Line 37: | Line 122: | ||
<ref name=RothTriangles><bibtex> | <ref name=RothTriangles><bibtex> | ||
@article{RothTriangles, | @article{RothTriangles, | ||
| − | author = | + | author = "Rothemund, Paul W. K AND Papadakis, Nick AND Winfree, Erik", |
| − | journal = | + | journal = "PLoS Biol", |
| − | publisher = | + | publisher = "Public Library of Science", |
| − | title = | + | title = "Algorithmic Self-Assembly of DNA Sierpinski Triangles", |
| − | year = | + | year = "2004", |
| − | month = | + | month = "12", |
| − | volume = | + | volume = "2", |
| − | url = | + | url = "http://dx.doi.org/10.1371%2Fjournal.pbio.0020424", |
| − | pages = | + | pages = "e424", |
| − | abstract = | + | abstract = " |
<p>Engineered DNA self-assembly to produce a fractal pattern demonstrates all the necessary mechanisms for the molecular implementation of arbitrary cellular automata.</p> | <p>Engineered DNA self-assembly to produce a fractal pattern demonstrates all the necessary mechanisms for the molecular implementation of arbitrary cellular automata.</p> | ||
| − | + | ", | |
| − | number = | + | number = "12", |
doi = {10.1371/journal.pbio.0020424} | doi = {10.1371/journal.pbio.0020424} | ||
} | } | ||
| Line 108: | Line 193: | ||
[[Category: Tile Assembly Models]] | [[Category: Tile Assembly Models]] | ||
| + | [[Category:Self-assembly]] | ||
Latest revision as of 16:06, 27 May 2014
In reality, DNA tile self-assembly is a more complicated process than that modeled by the aTAM, and therefore a different model is required for a realistic simulation of the physical process of self-assembling DNA tiles. Whereas the aTAM is a great model for studying the capabilities and limitations of tile assembly, and for programming tile sets to understand issues related to computation and geometry, the kinetic Tile Assembly Model (kTAM) [1] was developed as a more physically realistic model for laboratory settings, and considers the reversible nature of self-assembly, factoring in the rates of association and dissociation of basic molecular elements (so-called monomers, or tiles) within the original framework provided by the aTAM. The kTAM describes the dynamics of assembly according to a set of reversible chemical reactions: A tile can attach to an assembly anywhere that it makes even a weak bond, and any tile can dissociate from the assembly at a rate dependent on the total strength with which it adheres to the assembly. In this section, we first give a more formal definition of the kTAM, then describe the types of errors that it captures, and then discuss several results which have successfully demonstrated methods for reducing those errors. Techniques such as those discussed below have been responsible for a rapid and steady decline in the frequency of errors seen in laboratory experiments, plummeting from error rates of 10% per tile in 2004 [2] to only 0.13% by 2009 [3], and continuing to shrink.
Model Definition
In the kTAM [1] [4] [5], a monomer tile can be added to the assembly with some association (forward) rate, or removed from the assembly with some dissociation (reverse) rate. Similar to the aTAM, only the singleton tiles are allowed to attach to, and in this case detach from, a seeded assembly. These rates are denoted by \(r_f\) and \(r_{r,b}\), respectively. At every available site on the perimeter of an assembly (i.e. the frontier), every possible monomer tile can associate to the assembly, regardless of whether the monomer is correct or not (i.e. whether or not the glues match). The forward rate depends only on the monomer tile concentration, \([monomer]\)\[\begin{eqnarray*} r_f = k_f[monomer] = k_f e^{-G_{mc}} \end{eqnarray*}\]
where \(G_{mc} > 0\) is the non-dimensional entropic cost of associating to an assembly. In the kTAM, for simplicity it is assumed that tile concentrations remain constant at \([monomer] = e^{-G_{mc}}\). Therefore, since the forward rate constant \(k_f\) is a constant, the entire forward rate \(r_f\) is also constant.
The reverse rate is dependent upon the binding strength b of the tile to the assembly, and in fact the relationship is exponential\[\begin{eqnarray*} r_{r,b} = k_{r,b} = k_f e^{-bG_{se}} \end{eqnarray*}\]
where \(G_{se}\) is the non-dimensional free energy cost of breaking a single bond and b is the number of "single-strength" bonds the tile has made.
The kTAM's equivalent to the aTAM's temperature \(\tau\) parameter is the ratio of the concentration of the tiles to the strength of their individual bonds, or \(G_{mc}/G_{se}\). As a simplifying assumption, the tile concentrations are considered to remain constant during assembly (despite the fact that singleton tiles will be transitioning from freely floating individual tiles to being attached to growing assemblies), which in turn causes the temperature parameter to remain constant. (It should be noted that despite this and other simplifying assumptions, the kTAM does in fact provide a quite accurate model of the systems observed in laboratory settings.) Because the kTAM allows for the binding of tiles whether or not their glues correctly match those on the boundary of a growing assembly, bindings which would be considered errors in the aTAM are possible. By lowering the ratio of \(G_{mc}/G_{se}\), which is intuitively similar to lowering the temperature \(\tau\) threshold in the aTAM, assembly happens more quickly but is more error prone. If the number of correct bonds that a tile has with an assembly, b, is less than \(\tau\), then a tile is more likely to detach than to attach.
Because the kTAM accurately models the behavior of DNA based tile self-assembly in the laboratory, most especially the common types of errors observed, it has provided an excellent foundation for work in error prevention and correction.
Error Types
In order to discuss the types of errors that can occur during self-assembly in the kTAM, we will refer to an example system which is designed to weakly self-assemble the Sierpinski triangle. See the figures to the right for details.
The errors that occur during assembly can be divided into three general types: 1) growth errors (or mismatch errors), 2) facet errors, and 3) nucleation errors [5]. A growth error, an example of which can be seen in the figures below, occurs when one or more sides of a tile which binds to an assembly have glues which do not match the adjacent glues (called glue mismatches). Such a tile may bind with insufficient strength to remain permanently bound, but before it has an opportunity to dissociate, a previously unoccupied neighboring position may be filled by a tile which binds without mismatches, thus resulting in an assembly where every tile has sufficient strength to remain permanently attached despite the mismatch. This essentially "locks" the incorrect tile into place and potentially allows assembly to proceed with an incorrectly placed tile which may cause further deviations from the desired shape or pattern. Somewhat similarly, a facet error also occurs on the edge of a growing assembly. A facet error (see figures below for an example) again occurs when a tile binds with insufficient strength for permanent attachment (but this time with no mismatches), and again is locked into place by a subsequent tile addition. The third type of errors, nucleation errors, occur when tiles aggregate with each other without any attachment to the seed structure, and thus 'seed' a new type of assembly.
Survey of Results
The ability of the kTAM to accurately model the errors seen in laboratory settings coupled with its clean theoretical definition make it an ideal model in which to study mechanisms of error prevention and correction. Additionally, the algorithmic nature of self-assembly in the kTAM provides the opportunity to effectively apply a variety of algorithms from seemingly unrelated fields such as data transmission to make kTAM systems more robust.
While simply adjusting the ratio of \(G_{mc}\) to \(G_{se}\) is sufficient to drive error rates arbitrarily low, that comes at the cost of a huge slow-down to the overall assembly process. The pages below consists of results which are focused on one or both of the dual goals of decreasing the rate of errors during assembly and minimizing assembly time.
Error Suppresion Via Block Replacement
References
- ↑ 1.0 1.1
Erik Winfree - Algorithmic Self-Assembly of DNA
- Ph.D. Thesis, California Institute of Technology , June 1998
- BibtexAuthor : Erik Winfree
Title : Algorithmic Self-Assembly of DNA
In : Ph.D. Thesis, California Institute of Technology -
Address :
Date : June 1998
- ↑
Rothemund, Paul W. K AND Papadakis, Nick AND Winfree, Erik - Algorithmic Self-Assembly of DNA Sierpinski Triangles
- ↑
Barish, Robert D., Schulman, Rebecca, Rothemund, Paul W. K., Winfree, Erik - {An information-bearing seed for nucleating algorithmic self-assembly}
- Proceedings of the National Academy of Sciences 106(15):6054--6059, @apr 2009
- http://dx.doi.org/10.1073/pnas.0808736106
BibtexAuthor : Barish, Robert D., Schulman, Rebecca, Rothemund, Paul W. K., Winfree, Erik
Title : {An information-bearing seed for nucleating algorithmic self-assembly}
In : Proceedings of the National Academy of Sciences -
Address :
Date : @apr 2009
- ↑
Erik Winfree, Renat Bekbolatov - Proofreading Tile Sets: Error Correction for Algorithmic Self-Assembly.
- ↑ 5.0 5.1
Fujibayashi, Kenichi, Zhang, David Yu, Winfree, Erik, Murata, Satoshi - Error suppression mechanisms for DNA tile self-assembly and their simulation
- Natural Computing: an international journal 8(3):589--612, Hingham, MA, USA,2009
- BibtexAuthor : Fujibayashi, Kenichi, Zhang, David Yu, Winfree, Erik, Murata, Satoshi
Title : Error suppression mechanisms for DNA tile self-assembly and their simulation
In : Natural Computing: an international journal -
Address : Hingham, MA, USA
Date : 2009