Difference between revisions of "Building n by n squares"
Jhendricks (talk | contribs) (→Building $n \times n$ squares) |
|||
| (27 intermediate revisions by one other user not shown) | |||
| Line 4: | Line 4: | ||
Since Winfree showed in his thesis <ref name=Winf98 /> that the aTAM is computationally universal, we know that we can algorithmically direct the growth of assemblies. This ability allows for not only the creation of complicated and precise shapes, but also often for them to be created very tile type efficiently (i.e. they require small tile sets - those with few numbers of unique tile types). A benchmark problem for tile-based self-assembly is that of assembling an $n \times n$ square since this requires that the tiles somehow compute the value of $n$ and thus "know when to stop" at the boundaries. In <ref name =RotWin00 /> Rothemund and Winfree showed that binary counters can be used to guide the growth of squares and that thereby it is possible to self-assemble an $n \times n$ square using $O(\log n)$ tile types. | Since Winfree showed in his thesis <ref name=Winf98 /> that the aTAM is computationally universal, we know that we can algorithmically direct the growth of assemblies. This ability allows for not only the creation of complicated and precise shapes, but also often for them to be created very tile type efficiently (i.e. they require small tile sets - those with few numbers of unique tile types). A benchmark problem for tile-based self-assembly is that of assembling an $n \times n$ square since this requires that the tiles somehow compute the value of $n$ and thus "know when to stop" at the boundaries. In <ref name =RotWin00 /> Rothemund and Winfree showed that binary counters can be used to guide the growth of squares and that thereby it is possible to self-assemble an $n \times n$ square using $O(\log n)$ tile types. | ||
| − | + | [[File:square.png|thumb|right|360px|The high level schematic for building an $n \times n$ square using $O(\log n)$ tile types]] | |
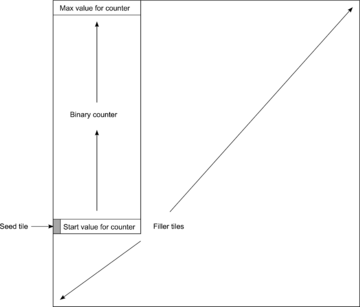
| − | + | The figure on the right shows a high-level overview of the construction. Essentially, $\log n$ tile types are required so that each bit of (a number related to) the dimension $n$ can be encoded with a unique tile type. The seed is taken to be one of those tile types so that the row of them forms attached to the seed. Above that, a fixed-width binary counter (which is composed of the same constant set of tile types regardless of $n$) begins counting upward from that value until it reaches its maximum possible value (i.e. all $1$'s), at which point it terminates upward growth. With the vertical bar representing the counter in place, a very basic constant (for all $n$) set of tiles can be used to "pass a signal" along a diagonal path which is limited by the height (and width) of the counter, and to finally fill in below the diagonal to finish the formation of the square. | |
| + | |||
| + | In <ref name=AdChGoHu01/>, Adleman, Cheng, Goel, and Huang improved the previous construction for squares to require the slightly fewer $O\left(\frac{\log n}{\log \log n}\right)$ tile types, which was also proven to be a matching lower bound (for almost all $n$) by using an information theoretic argument. | ||
| + | |||
| + | Note that while squares can be quite efficiently self-assembled, the tile complexity of lines and rectangles differs. For instance, the tile complexity lower bounds for $1 \times n$ lines is $n$, and for $k \times n$ rectangles (where $k \le n)$ is $\frac{n^{1/k}}{k}$ (which was shown by Cheng, Aggarwal, Goldwasser, Kao, Schweller, and Moisset de Espanés in <ref name=AGKS05g />). | ||
| + | |||
| + | As another measure of efficiency, Becker, Rémila, and Schabanel <ref name=BeckerTimeOpt/> considered the time required for squares (and cubes) to self-assemble. Of course, for this they had to consider that growth of the assembly need not be constrained to single tile additions at each step (since in that case an $n \times n$ square would clearly take $n^2-1$ time steps to grow from a single seed tile), but instead used a model equivalent to one in which every tile which can individually attach at any given step simultaneously attaches (rather than having just one of them nondeterministically chosen as in the regular aTAM). They were able to produce constructions for time optimal assembly of $n \times n$ squares in $2n - 2$ assembly steps. | ||
==References== | ==References== | ||
| Line 35: | Line 41: | ||
</bibtex></ref> | </bibtex></ref> | ||
| − | <ref name = | + | <ref name =AdChGoHu01><bibtex> |
| − | @ | + | @article{AdChGoHu01, |
| − | + | author = "Leonard Adleman, Qi Cheng, Ashish Goel, and Ming-Deh Huang", | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
year = "2001", | year = "2001", | ||
| − | + | title = "Running time and program size for self-assembled squares", | |
| − | + | booktitle = "Proceedings of the 33rd Annual ACM Symposium on Theory of Computing", | |
| + | publisher = "ACM" | ||
| + | pages = {740--748} | ||
} | } | ||
</bibtex></ref> | </bibtex></ref> | ||
| − | <ref name = | + | <ref name =AGKS05g><bibtex> |
| − | @article{ | + | @article{AGKS05g, |
| − | author = | + | author = "Qi Cheng, Gagan Aggarwal, Michael H. Goldwasser, Ming-Yang Kao, Robert T. Schweller, and Pablo Moisset de Espanés", |
| − | + | year = "2005", | |
| − | + | title = "Complexities for generalized models of self-assembly", | |
| − | + | journal = "SIAM Journal on Computing", | |
| − | + | volume = "34", | |
| − | pages = | + | pages = {1493--1515} |
} | } | ||
| − | |||
</bibtex></ref> | </bibtex></ref> | ||
| − | <ref name = | + | <ref name =BeckerTimeOpt><bibtex> |
| − | @article{ | + | @article{BeckerTimeOpt, |
| − | author | + | author = "Florent Becker, Éric Rémila, and Nicolas Schabanel", |
| − | + | year = "2008", | |
| − | + | month = "June" | |
| − | + | title = "Time optimal self-assembly for 2d and 3d shapes: The case of squares and cubes", | |
| − | + | journal = "DNA Computing", | |
| − | + | volume = "14", | |
| − | + | pages = {144--155} | |
| − | pages = { | ||
| − | |||
| − | |||
} | } | ||
</bibtex></ref> | </bibtex></ref> | ||
| + | |||
</references> | </references> | ||
| + | |||
| + | [[Category:Results in the aTAM]] | ||
| + | [[Category:Self-assembly]] | ||
Latest revision as of 15:15, 27 May 2014
Building \(n \times n\) squares
Since Winfree showed in his thesis [1] that the aTAM is computationally universal, we know that we can algorithmically direct the growth of assemblies. This ability allows for not only the creation of complicated and precise shapes, but also often for them to be created very tile type efficiently (i.e. they require small tile sets - those with few numbers of unique tile types). A benchmark problem for tile-based self-assembly is that of assembling an \(n \times n\) square since this requires that the tiles somehow compute the value of \(n\) and thus "know when to stop" at the boundaries. In [2] Rothemund and Winfree showed that binary counters can be used to guide the growth of squares and that thereby it is possible to self-assemble an \(n \times n\) square using \(O(\log n)\) tile types.
The figure on the right shows a high-level overview of the construction. Essentially, \(\log n\) tile types are required so that each bit of (a number related to) the dimension \(n\) can be encoded with a unique tile type. The seed is taken to be one of those tile types so that the row of them forms attached to the seed. Above that, a fixed-width binary counter (which is composed of the same constant set of tile types regardless of \(n\)) begins counting upward from that value until it reaches its maximum possible value (i.e. all \(1\)'s), at which point it terminates upward growth. With the vertical bar representing the counter in place, a very basic constant (for all \(n\)) set of tiles can be used to "pass a signal" along a diagonal path which is limited by the height (and width) of the counter, and to finally fill in below the diagonal to finish the formation of the square.
In [3], Adleman, Cheng, Goel, and Huang improved the previous construction for squares to require the slightly fewer \(O\left(\frac{\log n}{\log \log n}\right)\) tile types, which was also proven to be a matching lower bound (for almost all \(n\)) by using an information theoretic argument.
Note that while squares can be quite efficiently self-assembled, the tile complexity of lines and rectangles differs. For instance, the tile complexity lower bounds for \(1 \times n\) lines is \(n\), and for \(k \times n\) rectangles (where \(k \le n)\) is \(\frac{n^{1/k}}{k}\) (which was shown by Cheng, Aggarwal, Goldwasser, Kao, Schweller, and Moisset de Espanés in [4]).
As another measure of efficiency, Becker, Rémila, and Schabanel [5] considered the time required for squares (and cubes) to self-assemble. Of course, for this they had to consider that growth of the assembly need not be constrained to single tile additions at each step (since in that case an \(n \times n\) square would clearly take \(n^2-1\) time steps to grow from a single seed tile), but instead used a model equivalent to one in which every tile which can individually attach at any given step simultaneously attaches (rather than having just one of them nondeterministically chosen as in the regular aTAM). They were able to produce constructions for time optimal assembly of \(n \times n\) squares in \(2n - 2\) assembly steps.
References
- ↑
Erik Winfree - Algorithmic Self-Assembly of DNA
- Ph.D. Thesis, California Institute of Technology , June 1998
- BibtexAuthor : Erik Winfree
Title : Algorithmic Self-Assembly of DNA
In : Ph.D. Thesis, California Institute of Technology -
Address :
Date : June 1998
- ↑
Paul W. K. Rothemund, Erik Winfree - The Program-size Complexity of Self-Assembled Squares (extended abstract)
- STOC '00: Proceedings of the thirty-second annual ACM Symposium on Theory of Computing pp. 459--468, Portland, Oregon, United States,2000
- BibtexAuthor : Paul W. K. Rothemund, Erik Winfree
Title : The Program-size Complexity of Self-Assembled Squares (extended abstract)
In : STOC '00: Proceedings of the thirty-second annual ACM Symposium on Theory of Computing -
Address : Portland, Oregon, United States
Date : 2000
- ↑
Leonard Adleman, Qi Cheng, Ashish Goel,, Ming-Deh Huang - Running time and program size for self-assembled squares
- ↑
Qi Cheng, Gagan Aggarwal, Michael H. Goldwasser, Ming-Yang Kao, Robert T. Schweller,, Pablo Moisset de Espanés - Complexities for generalized models of self-assembly
- ↑
Florent Becker, Éric Rémila,, Nicolas Schabanel - Time optimal self-assembly for 2d and 3d shapes: The case of squares and cubes